2.5.7: Proof-Theoretic Notions

\(\def\Assign#1#2{ { #1^{\Struct{#2}} } }\)
\(\def\Atom#1#2{ { \mathord{#1}(#2) } }\)
\(\def\Bin{ {\mathbb{B}} }\)
\(\def\cardeq#1#2{ { #1 \approx #2 } }\)
\(\def\cardle#1#2{ { #1 \preceq #2 } }\)
\(\def\cardless#1#2{ { #1 \prec #2 } }\)
\(\def\cardneq#1#2{ { #1 \not\approx #2 } }\)
\(\def\comp#1#2{ { #2 \circ #1 } }\)
\(\def\concat{ { \;\frown\; } }\)
\(\def\Cut{ { \text{Cut} } }\)
\(\def\Discharge#1#2{ { [#1]^#2 } }\)
\(\def\DischargeRule#1#2{ { \RightLabel{#1}\LeftLabel{\scriptsize{#2} } } }\)
\(\def\dom#1{ {\operatorname{dom}(#1)} }\)
\(\def\Domain#1{ {\left| \Struct{#1} \right|} }\)
\(\def\Elim#1{ { {#1}\mathrm{Elim} } }\)
\(\newcommand{\Entails}{\vDash}\)
\(\newcommand{\EntailsN}{\nvDash}\)
\(\def\eq[#1][#2]{ { #1 = #2 } }\)
\(\def\eqN[#1][#2]{ { #1 \neq #2 } }\)
\(\def\equivclass#1#2{ { #1/_{#2} } }\)
\(\def\equivrep#1#2{ { [#1]_{#2} } }\)
\(\def\Exchange{ { \text{X} } }\)
\(\def\False{ { \mathbb{F} } }\)
\(\def\FalseCl{ { \lfalse_C } }\)
\(\def\FalseInt{ { \lfalse_I } }\)
\(\def\fCenter{ { \,\Sequent\, } }\)
\(\def\fdefined{ { \;\downarrow } }\)
\(\def\fn#1{ { \operatorname{#1} } }\)
\(\def\Frm[#1]{ {\operatorname{Frm}(\Lang #1)} }\)
\(\def\fundefined{ { \;\uparrow } }\)
\(\def\funimage#1#2{ { #1[#2] } }\)
\(\def\funrestrictionto#1#2{ { #1 \restriction_{#2} } }\)
\(\newcommand{\ident}{\equiv}\)
\(\newcommand{\indcase}[2]{#1 \ident #2\text{:}}\)
\(\newcommand{\indcaseA}[2]{#1 \text{ is atomic:}}\)
\(\def\indfrm{ { A } }\)
\(\def\indfrmp{ { A } }\)
\(\def\joinrel{\mathrel{\mkern-3mu}}\)
\(\def\lambd[#1][#2]{\lambda #1 . #2}\)
\(\def\Lang#1{ { \mathcal{#1} } }\)
\(\def\LeftR#1{ { {#1}\mathrm{L} } }\)
\(\def\len#1{ {\operatorname{len}(#1)} }\)
\(\def\lexists#1#2{ { \exists #1\, #2 } }\)
\(\def\lfalse{ {\bot} }\)
\(\def\lforall#1#2{ { \forall#1\, #2 } }\)
\(\newcommand{\lif}{\rightarrow}\)
\(\newcommand{\liff}{\leftrightarrow}\)
\(\def\Log#1{ { \mathbf{#1} } }\)
\(\def\ltrue{ {\top} }\)
\(\def\Id#1{ {\operatorname{Id}_#1} }\)
\(\def\Int{ {\mathbb{Z}} }\)
\(\def\Intro#1{ { {#1}\mathrm{Intro} } }\)
\(\def\mModel#1{ { \mathfrak{#1} } }\)
\(\newcommand{\mSat}[3][{}]{\mModel{#2}{#1}\Vdash{#3}}\)
\(\newcommand{\mSatN}[3][{}]{\mModel{#2}{#1}\nVdash{#3}}\)
\(\def\Nat{ {\mathbb{N}} }\)
\(\def\nicefrac#1#2{ {{}^#1/_#2} }\)
\(\def\num#1{ { \overline{#1} } }\)

\(\def\ran#1{ {\operatorname{ran}(#1)} }\)
\(\newcommand{\Obj}[1]{\mathsf{#1}}\)
\(\def\Rat{ {\mathbb{Q}} }\)
\(\def\Real{ {\mathbb{R}} }\)
\(\def\RightR#1{ { {#1}\mathrm{R} } }\)
\(\def\Part#1#2{ { \Atom{\Obj P}{#1, #2} } }\)
\(\def\pto{ { \hspace{0.1 cm}\to\hspace{-0.44 cm}\vcenter{\tiny{\hbox{|}}}\hspace{0.35 cm} } }\)
\(\def\PosInt{ {\mathbb{Z}^+} }\)
\(\def\Pow#1{ {\wp(#1)} }\)
\(\newcommand{\Proves}{\vdash}\)
\(\newcommand{\ProvesN}{\nvdash}\)
\(\def\Relbar{\mathrel{=}}\)
\(\newcommand{\Sat}[3][{}]{\Struct{#2}{#1}\vDash{#3}}\)
\(\newcommand{\SatN}[3][{}]{\Struct{#2}{#1}\nvDash{#3}}\)
\(\newcommand{\Sequent}{\Rightarrow}\)
\(\def\Setabs#1#2{ { \{#1:#2\} } }\)
\(\newcommand{\sFmla}[2]{#1\,#2}\)
\(\def\Struct#1{ {#1} }\)
\(\def\subst#1#2{ { #1/#2 } }\)
\(\def\Subst#1#2#3{ { #1[\subst{#2}{#3}] } }\)
\(\def\TMblank{ { 0 } }\)
\(\newcommand{\TMendtape}{\triangleright}\)
\(\def\TMleft{ { L } }\)
\(\def\TMright{ { R } }\)
\(\def\TMstay{ { N } }\)
\(\def\TMstroke{ { 1 } }\)
\(\def\TMtrans#1#2#3{ { #1,#2,#3 } }\)
\(\def\Trm[#1]{ {\operatorname{Trm}(\Lang #1)} }\)
\(\def\True{ { \mathbb{T} } }\)
\(\newcommand{\TRule}[2]{#2#1}\)
\(\def\tuple#1{ {\langle #1 \rangle} }\)
\(\newcommand{\Value}[3][\,]{\mathrm{Val}_{#1}^{#3}(#2)}\)
\(\def\Var{ { \mathrm{Var} } }\)
\(\newcommand{\varAssign}[3]{#1 \sim_{#3} #2}\)
\(\def\Weakening{ { \text{W} } }\)

Just as we’ve defined a number of important semantic notions (validity, entailment, satisfiability), we now define corresponding proof-theoretic notions. These are not defined by appeal to satisfaction of sentences in structures, but by appeal to the derivability or non-derivability of certain sentences from others. It was an important discovery that these notions coincide. That they do is the content of the soundness and completeness theorems.

Definition \(\PageIndex{1}\): Theorems

A sentence \(A\) is a theorem if there is a derivation of \(A\) in natural deduction in which all assumptions are discharged. We write \(\Proves A\) if \(A\) is a theorem and \(\ProvesN A\) if it is not.

Definition \(\PageIndex{2}\): Derivability

A sentence \(A\) is derivable from a set of sentences \(\Gamma\), \(\Gamma \Proves A\), if there is a derivation with conclusion \(A\) and in which every assumption is either discharged or is in \(\Gamma\). If \(A\) is not derivable from \(\Gamma\) we write \(\Gamma \ProvesN A\).

Definition \(\PageIndex{3}\): Consistency

A set of sentences \(\Gamma\) is inconsistent iff \(\Gamma \Proves \lfalse\). If \(\Gamma\) is not inconsistent, i.e., if \(\Gamma \ProvesN \lfalse\), we say it is consistent.

Proposition \(\PageIndex{1}\): Reflexivity

If \(A \in \Gamma\), then \(\Gamma \Proves A\).

Proof. The assumption \(A\) by itself is a derivation of \(A\) where every undischarged assumption (i.e., \(A\)) is in \(\Gamma\). ◻

Proposition \(\PageIndex{2}\): Monotony

If \(\Gamma \subseteq \Delta\) and \(\Gamma \Proves A\), then \(\Delta \Proves A\).

Proof. Any derivation of \(A\) from \(\Gamma\) is also a derivation of \(A\) from \(\Delta\). ◻

Proposition \(\PageIndex{3}\): Transitivity

If \(\Gamma \Proves A\) and \(\{A\} \cup \Delta \Proves B\), then \(\Gamma \cup \Delta \Proves B\).

Proof. If \(\Gamma \Proves A\), there is a derivation \(\delta_0\) of \(A\) with all undischarged assumptions in \(\Gamma\). If \(\{A\} \cup \Delta \Proves B\), then there is a derivation \(\delta_1\) of \(B\) with all undischarged assumptions in \(\{A\} \cup \Delta\). Now consider:

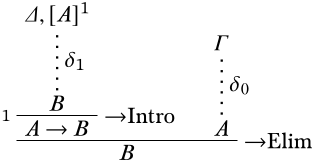
The undischarged assumptions are now all among \(\Gamma \cup \Delta\), so this shows \(\Gamma \cup \Delta \Proves B\). ◻

When \(\Gamma = \{A_1, A_2, \ldots, A_k\}\) is a finite set we may use the simplified notation \(A_1,A_2,\ldots,A_k \Proves B\) for \(\Gamma \Proves B\), in particular \(A \Proves B\) means that \(\{A\} \Proves B\).

Note that if \(\Gamma \Proves A\) and \(A \Proves B\), then \(\Gamma \Proves B\). It follows also that if \(A_1, \dots, A_n \Proves B\) and \(\Gamma \Proves A_i\) for each \(i\), then \(\Gamma \Proves B\).

Proposition \(\PageIndex{4}\)

The following are equivalent.

1. \(\Gamma\) is inconsistent.
2. \(\Gamma \Proves {A}\) for every sentence \({A}\).
3. \(\Gamma \Proves {A}\) and \(\Gamma \Proves \lnot {A}\) for some sentence \({A}\).

Proof. Exercise. ◻

Problem \(\PageIndex{1}\)

Prove Proposition \(\PageIndex{4}\).

Proposition \(\PageIndex{5}\): Compactness

1. If \(\Gamma \Proves A\) then there is a finite subset \(\Gamma_0 \subseteq \Gamma\) such that \(\Gamma_0 \Proves A\).
2. If every finite subset of \(\Gamma\) is consistent, then \(\Gamma\) is consistent.

Proof.

1. If \(\Gamma \Proves A\), then there is a derivation \(\delta\) of \(A\) from \(\Gamma\). Let \(\Gamma_0\) be the set of undischarged assumptions of \(\delta\). Since any derivation is finite, \(\Gamma_0\) can only contain finitely many sentences. So, \(\delta\) is a derivation of \(A\) from a finite \(\Gamma_0 \subseteq \Gamma\).
2. This is the contrapositive of (1) for the special case \(A \ident \lfalse\).

◻