2.5.6: Derivations with Quantifiers

\(\def\Assign#1#2{ { #1^{\Struct{#2}} } }\)
\(\def\Atom#1#2{ { \mathord{#1}(#2) } }\)
\(\def\Bin{ {\mathbb{B}} }\)
\(\def\cardeq#1#2{ { #1 \approx #2 } }\)
\(\def\cardle#1#2{ { #1 \preceq #2 } }\)
\(\def\cardless#1#2{ { #1 \prec #2 } }\)
\(\def\cardneq#1#2{ { #1 \not\approx #2 } }\)
\(\def\comp#1#2{ { #2 \circ #1 } }\)
\(\def\concat{ { \;\frown\; } }\)
\(\def\Cut{ { \text{Cut} } }\)
\(\def\Discharge#1#2{ { [#1]^#2 } }\)
\(\def\DischargeRule#1#2{ { \RightLabel{#1}\LeftLabel{\scriptsize{#2} } } }\)
\(\def\dom#1{ {\operatorname{dom}(#1)} }\)
\(\def\Domain#1{ {\left| \Struct{#1} \right|} }\)
\(\def\Elim#1{ { {#1}\mathrm{Elim} } }\)
\(\newcommand{\Entails}{\vDash}\)
\(\newcommand{\EntailsN}{\nvDash}\)
\(\def\eq[#1][#2]{ { #1 = #2 } }\)
\(\def\eqN[#1][#2]{ { #1 \neq #2 } }\)
\(\def\equivclass#1#2{ { #1/_{#2} } }\)
\(\def\equivrep#1#2{ { [#1]_{#2} } }\)
\(\def\Exchange{ { \text{X} } }\)
\(\def\False{ { \mathbb{F} } }\)
\(\def\FalseCl{ { \lfalse_C } }\)
\(\def\FalseInt{ { \lfalse_I } }\)
\(\def\fCenter{ { \,\Sequent\, } }\)
\(\def\fdefined{ { \;\downarrow } }\)
\(\def\fn#1{ { \operatorname{#1} } }\)
\(\def\Frm[#1]{ {\operatorname{Frm}(\Lang #1)} }\)
\(\def\fundefined{ { \;\uparrow } }\)
\(\def\funimage#1#2{ { #1[#2] } }\)
\(\def\funrestrictionto#1#2{ { #1 \restriction_{#2} } }\)
\(\newcommand{\ident}{\equiv}\)
\(\newcommand{\indcase}[2]{#1 \ident #2\text{:}}\)
\(\newcommand{\indcaseA}[2]{#1 \text{ is atomic:}}\)
\(\def\indfrm{ { A } }\)
\(\def\indfrmp{ { A } }\)
\(\def\joinrel{\mathrel{\mkern-3mu}}\)
\(\def\lambd[#1][#2]{\lambda #1 . #2}\)
\(\def\Lang#1{ { \mathcal{#1} } }\)
\(\def\LeftR#1{ { {#1}\mathrm{L} } }\)
\(\def\len#1{ {\operatorname{len}(#1)} }\)
\(\def\lexists#1#2{ { \exists #1\, #2 } }\)
\(\def\lfalse{ {\bot} }\)
\(\def\lforall#1#2{ { \forall#1\, #2 } }\)
\(\newcommand{\lif}{\rightarrow}\)
\(\newcommand{\liff}{\leftrightarrow}\)
\(\def\Log#1{ { \mathbf{#1} } }\)
\(\def\ltrue{ {\top} }\)
\(\def\Id#1{ {\operatorname{Id}_#1} }\)
\(\def\Int{ {\mathbb{Z}} }\)
\(\def\Intro#1{ { {#1}\mathrm{Intro} } }\)
\(\def\mModel#1{ { \mathfrak{#1} } }\)
\(\newcommand{\mSat}[3][{}]{\mModel{#2}{#1}\Vdash{#3}}\)
\(\newcommand{\mSatN}[3][{}]{\mModel{#2}{#1}\nVdash{#3}}\)
\(\def\Nat{ {\mathbb{N}} }\)
\(\def\nicefrac#1#2{ {{}^#1/_#2} }\)
\(\def\num#1{ { \overline{#1} } }\)

\(\def\ran#1{ {\operatorname{ran}(#1)} }\)
\(\newcommand{\Obj}[1]{\mathsf{#1}}\)
\(\def\Rat{ {\mathbb{Q}} }\)
\(\def\Real{ {\mathbb{R}} }\)
\(\def\RightR#1{ { {#1}\mathrm{R} } }\)
\(\def\Part#1#2{ { \Atom{\Obj P}{#1, #2} } }\)
\(\def\pto{ { \hspace{0.1 cm}\to\hspace{-0.44 cm}\vcenter{\tiny{\hbox{|}}}\hspace{0.35 cm} } }\)
\(\def\PosInt{ {\mathbb{Z}^+} }\)
\(\def\Pow#1{ {\wp(#1)} }\)
\(\newcommand{\Proves}{\vdash}\)
\(\newcommand{\ProvesN}{\nvdash}\)
\(\def\Relbar{\mathrel{=}}\)
\(\newcommand{\Sat}[3][{}]{\Struct{#2}{#1}\vDash{#3}}\)
\(\newcommand{\SatN}[3][{}]{\Struct{#2}{#1}\nvDash{#3}}\)
\(\newcommand{\Sequent}{\Rightarrow}\)
\(\def\Setabs#1#2{ { \{#1:#2\} } }\)
\(\newcommand{\sFmla}[2]{#1\,#2}\)
\(\def\Struct#1{ {#1} }\)
\(\def\subst#1#2{ { #1/#2 } }\)
\(\def\Subst#1#2#3{ { #1[\subst{#2}{#3}] } }\)
\(\def\TMblank{ { 0 } }\)
\(\newcommand{\TMendtape}{\triangleright}\)
\(\def\TMleft{ { L } }\)
\(\def\TMright{ { R } }\)
\(\def\TMstay{ { N } }\)
\(\def\TMstroke{ { 1 } }\)
\(\def\TMtrans#1#2#3{ { #1,#2,#3 } }\)
\(\def\Trm[#1]{ {\operatorname{Trm}(\Lang #1)} }\)
\(\def\True{ { \mathbb{T} } }\)
\(\newcommand{\TRule}[2]{#2#1}\)
\(\def\tuple#1{ {\langle #1 \rangle} }\)
\(\newcommand{\Value}[3][\,]{\mathrm{Val}_{#1}^{#3}(#2)}\)
\(\def\Var{ { \mathrm{Var} } }\)
\(\newcommand{\varAssign}[3]{#1 \sim_{#3} #2}\)
\(\def\Weakening{ { \text{W} } }\)

Example \(\PageIndex{1}\)

When dealing with quantifiers, we have to make sure not to violate the eigenvariable condition, and sometimes this requires us to play around with the order of carrying out certain inferences. In general, it helps to try and take care of rules subject to the eigenvariable condition first (they will be lower down in the finished proof).

Let’s see how we’d give a derivation of the formula \(\lexists{x}{\lnot A(x)} \lif \lnot \lforall{x}{A(x)}\). Starting as usual, we write

We start by writing down what it would take to justify that last step using the \(\Intro{\lif}\) rule.

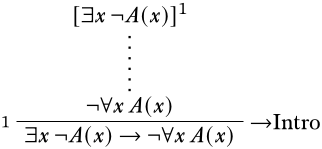
Since there is no obvious rule to apply to \(\lnot \lforall{x}{A(x)}\), we will proceed by setting up the derivation so we can use the \(\Elim{\lexists{}{}}\) rule. Here we must pay attention to the eigenvariable condition, and choose a constant that does not appear in \(\lexists{x}{A(x)}\) or any assumptions that it depends on. (Since no constant symbols appear, however, any choice will do fine.)

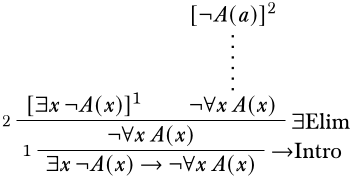
In order to derive \(\lnot \lforall{x}{A(x)}\), we will attempt to use the \(\Intro{\lnot}\) rule: this requires that we derive a contradiction, possibly using \(\lforall{x}{A(x)}\) as an additional assumption. Of course, this contradiction may involve the assumption \(\lnot A(a)\) which will be discharged by the \(\Intro{\lif}\) inference. We can set it up as follows:

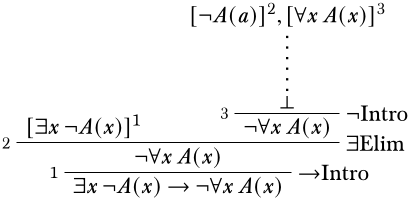
It looks like we are close to getting a contradiction. The easiest rule to apply is the \(\Elim{\lforall{}{}}\), which has no eigenvariable conditions. Since we can use any term we want to replace the universally quantified \(x\), it makes the most sense to continue using \(a\) so we can reach a contradiction.

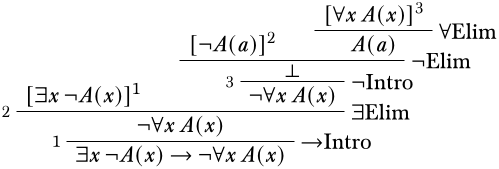
It is important, especially when dealing with quantifiers, to double check at this point that the eigenvariable condition has not been violated. Since the only rule we applied that is subject to the eigenvariable condition was \(\Elim{\exists}\), and the eigenvariable \(a\) does not occur in any assumptions it depends on, this is a correct derivation.

Example \(\PageIndex{2}\)

Sometimes we may derive a formula from other formulas. In these cases, we may have undischarged assumptions. It is important to keep track of our assumptions as well as the end goal.

Let’s see how we’d give a derivation of the formula \(\lexists{x}{C(x,b)}\) from the assumptions \(\lexists{x}{(A(x) \land B(x))}\) and \(\lforall{x}{(B(x) \lif C(x,b))}\). Starting as usual, we write the conclusion at the bottom.

We have two premises to work with. To use the first, i.e., try to find a derivation of \(\lexists{x}{C(x, b)}\) from \(\lexists{x}{(A(x) \land B(x))}\) we would use the \(\Elim{\lexists{}{}}\) rule. Since it has an eigenvariable condition, we will apply that rule first. We get the following:

The two assumptions we are working with share \(B\). It may be useful at this point to apply \(\Elim{\land}\) to separate out \(B(a)\).

The second assumption we have to work with is \(\lforall{x}{(B(x) \lif C(x,b))}\). Since there is no eigenvariable condition we can instantiate \(x\) with the constant symbol \(a\) using \(\Elim{\lforall{}{}}\) to get \(B(a) \lif C(a, b)\). We now have both \(B(a) \lif C(a,b)\) and \(B(a)\). Our next move should be a straightforward application of the \(\Elim{\lif}\) rule.

We are so close! One application of \(\Intro{\lexists{}{}}\) and we have reached our goal.

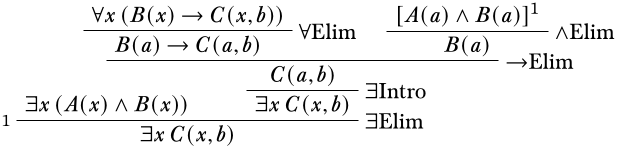
Since we ensured at each step that the eigenvariable conditions were not violated, we can be confident that this is a correct derivation.

Example \(\PageIndex{3}\)

Give a derivation of the formula \(\lnot\lforall{x}{A(x)}\) from the assumptions \(\lforall{x}{A(x)} \lif \lexists{y}{B(y)}\) and \(\lnot\lexists{y}{B(y)}\). Starting as usual, we write the target formula at the bottom.

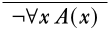
The last line of the derivation is a negation, so let’s try using \(\Intro{\lnot}\). This will require that we figure out how to derive a contradiction.

So far so good. We can use \(\Elim{\lforall{}{}}\) but it’s not obvious if that will help us get to our goal. Instead, let’s use one of our assumptions. \(\lforall{x}{A(x)} \lif \lexists{y}{B(y)}\) together with \(\lforall{x}{A(x)}\) will allow us to use the \(\Elim{\lif}\) rule.

We now have one final assumption to work with, and it looks like this will help us reach a contradiction by using \(\Elim{\lnot}\).

Problem \(\PageIndex{1}\)

Give derivations of the following:

1. \(\lexists{y}{A(y)} \lif B\) from the assumption \(\lforall{x}{(A(x) \lif B)}\)
2. \(\lexists{x}{(A(x) \lif \lforall{y}{A(y)})}\)