A categorical syllogism is just an argument with two premises and a conclusion, where every statement of the argument is a categorical statement. As we have seen, there are four different types (forms) of categorical statement:
All S are P (universal affirmative)
No S are P (universal negative)
Some S are P (particular affirmative)
Some S are not P (particular negative)
Thus, any categorical syllogism’s premises and conclusion will be some mixture of these different types of statement. The argument I gave at the beginning of section 2.13 was a categorical syllogism. Here, again, is that argument:
- All humans are mortal
- All mortal things die
- Therefore, all humans die
As we can see now that we have learned the four categorical forms, each one of the statements in this syllogism is a “universal affirmative” statement of the form, “all S are P.” Let’s first translate each statement of this argument to have the “all S are P” form:
- All humans are things that are mortal.
- All things that are mortal are things that die.
- ll humans are things that die.
In determining the validity of categorical syllogisms, we must construct a three category Venn diagram for the premises and a two category Venn diagram for the conclusion. Here is what the three category Venn looks like for the premises:
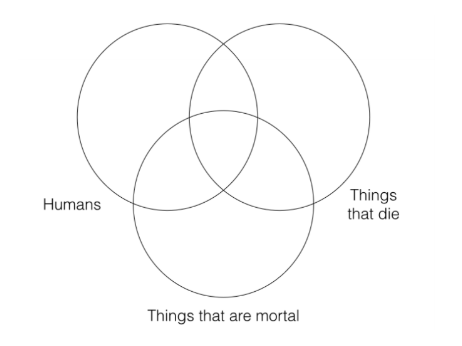
We need a three category Venn for the premises since the two premises refer to three different categories. The way you should construct the Venn is with the circle that represents the “S” category of the conclusion (i.e., the category “humans”) on left, the circle that represents the “P” category of the conclusion (i.e., the category “things that die”) on the right, and the remaining category (“things that are mortal”) in the middle, as I have done above. Constructing your three category Venn in this way will allow you to easily determine whether the argument is valid.
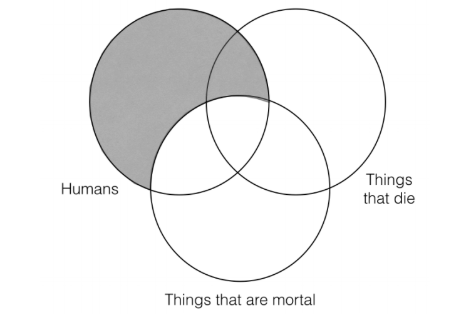
The next thing we must do is represent the information from the first two premises in our three category Venn. We’ll start with the first premise, which says “all humans are things that are mortal.” That means that we must shade out anything that is in the “human” category, but that isn’t in the “things that are mortal” category, like this:
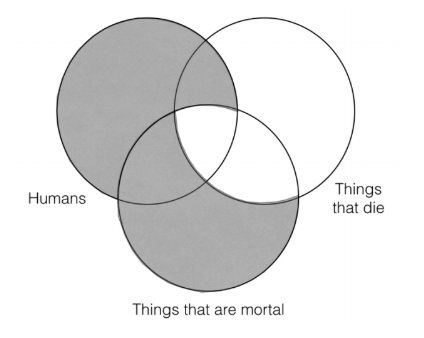
The next thing we have to do is fill in the information for the second premise, all things that are mortal are things that die. That means that there isn’t anything that is in the category “things that are mortal” but that isn’t in the “things that die” category. So we must shade out all of the parts of the “things that are mortal” category the lie outside the “things that die” category, like this:
The next thing we have to do is construct a two category Venn for the conclusion and then compare the information represented by the three category Venn for the premises to the two category Venn for the conclusion.
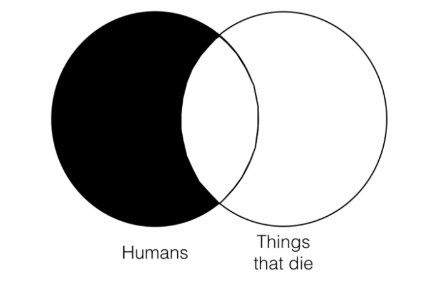
The conclusion represents the information that there is nothing in the “humans” category that isn’t also in the “things that die” category. It also allows that there are things that die, but that aren’t humans. The premise Venn also includes this same information, since every part of the “humans” category that is outside the “things that die” category is shaded out. Thus, this argument passes the Venn test of validity and is thus valid since there is no information represented in the conclusion Venn that is not also represented in the premise Venn. Notice that it doesn’t matter that the premise Venn contains more information than the conclusion Venn. That is to be expected, since the premise Venn is representing a whole other category that the conclusion Venn isn’t. This is perfectly allowable. What isn’t allowable (and thus would make an argument fail the Venn test of validity) is if the conclusion Venn contained information that wasn’t already contained in the premise Venn. However, since this argument does not do that, it is valid.
Let’s try another one.
- All pediatricians are doctors
- All pediatricians like children
- Therefore, all doctors like children.
The first step is to identify the three categories referred to in this categorical syllogism. They are:
Pediatricians
Doctors
Things that like children
The next step is to fill out the three category Venn for the premises and the two category Venn for the conclusion.

This argument does not pass the Venn test of validity because there is information contained in the conclusion Venn that is not contained in the premise Venn. In particular, the conclusion says that there is nothing in the “doctors” category that is outside the “things that like children category.” However, the premises do not represent that information, since the section of the category “doctors” that lies outside of the intersection of the category “things that like children” is unshaded, thus representing that there can be things there.
Sometimes when filling in particular statements on a three category for the premises, you will encounter a problem that requires another convention in order to accurately represent the information in the Venn. Here is an example where this happens:
- Some mammals are bears
- Some two-legged creatures are mammals
- Therefore, some two-legged creatures are bears
There are three categories referred to in this categorical syllogism:
Mammals
Bears
Two-legged creatures
As always, we will put the “S” term of the conclusion on the left of our three category Venn, the “P” term on the right, and the remaining term in the middle, as follows:
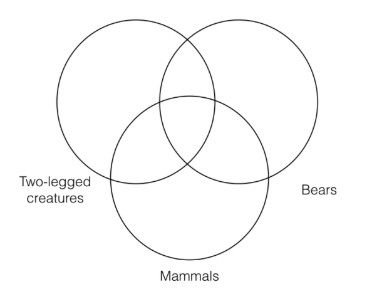
Now we need to represent the first premise, which means we need to put an asterisk in the intersection of the “mammals” and “bears” categories. However, here we have a choice to make. Since the intersection of the “bears” and “mammals” categories contains a section that is outside the “two-legged creatures” category and a section that is inside the “two-legged creatures” category, we must choose between representing the particular as part of the “two-legged creatures” category or not.

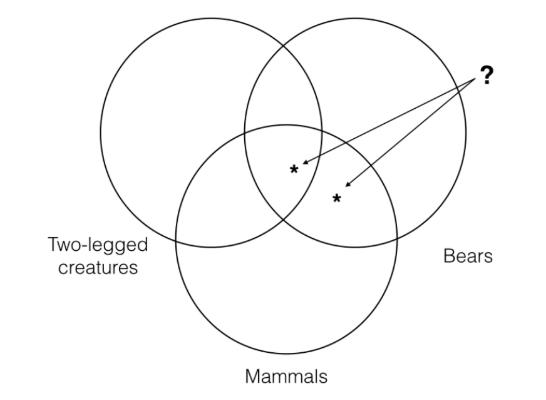
But neither of these can be right, since the first premise says nothing at all about whether the thing that is both a bear and a mammal is two-legged! Thus, in order to accurately represent the information contained in this premise, we must adopt a new convention. That convention says that when we encounter a situation where we must represent a particular on our three category Venn, but the premise says nothing about a particular category, then we must put the asterisk on the line of that category as I have done below. When we do this, it will represent that the particular is neither inside the category or outside the category.

We must do this same thing for the second premise, since we encounter the same problem there. Thus, when putting the asterisk in the intersection of the “two-legged creatures” and “mammals” categories, we cannot put the asterisk either inside or outside the “bears” category. Instead, we must put the asterisk on the line of the “bears” category. Thus, using this convention, we can represent the premise Venn and conclusion Venn as follows:
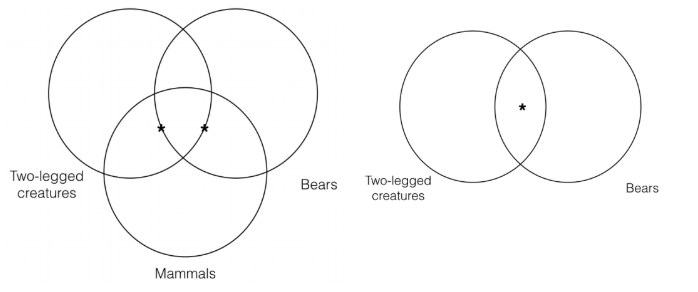
Keeping in mind the convention we have just introduced, we can see that this argument fails the Venn test of validity and is thus invalid. The reason is that the conclusion Venn clearly represents an individual in the intersection of the “two-legged creatures” and “bears” categories, whereas the premise Venn contains no such information. Thus, the conclusion Venn contains information that is not contained in the premise Venn, which means the argument is invalid.
We will close this section with one last example that will illustrate an important strategy. The strategy is that we should always map universal statements before mapping particular statements. Here is a categorical syllogism that illustrates this point. This time I am going to switch to just using the capital letters S, P, and M to represent the categories. Recall that we can do this because the Venn test of validity is a formal evaluation method where we don’t have to actually understand what the categories represent in the world in order to determine whether the argument is valid.
- Some S are M
- All M are P
- ∴ Some S are P
If we think about mapping the first premise on our three category Venn, it seems that we will have to utilize the convention we just introduced, since the first premise is a particular categorical statement that mentions only the categories S and M and nothing about the category P:
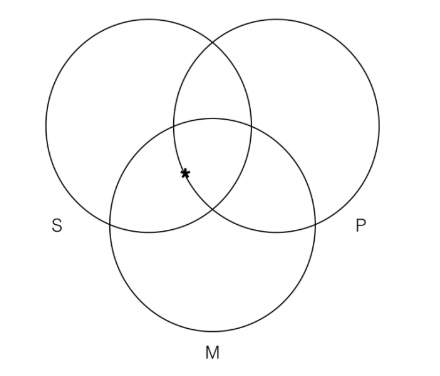
However, as it turns out, we don’t have to use this convention because when we map premise 2, which is a universal statement, this clears up where the asterisk has to go:
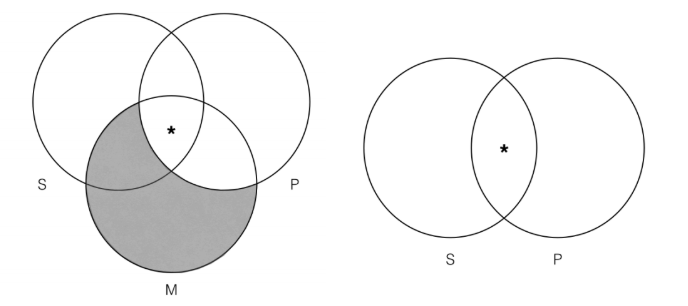
We can see that once we’ve mapped the universal statement onto the premise Venn (on the left), there is only one section where the asterisk can go that is in the intersection of S and M. The reason is that once we have mapped the “all M are P” premise, and have thus shaded out any portion of the M category that is outside the P category, we know that that asterisk cannot belong inside the M category, given that it has to be inside the P category. When we apply the Venn test of validity to the above argument, we can see that it is valid since the conclusion Venn does not contain any information that isn’t already contained in the premise Venn. The conclusion simply says that there is some thing that is both S and P, and that information is already represented in our premise Venn. Thus, the argument is valid. The point of strategy here is that we should always map our universal statements onto our three category Venns before mapping our particular statements. The reason is that the universal can determine how we map our particular statements (but not vice versa).
Exercise
Use the Venn test of validity to determine whether the following syllogisms are valid or invalid.
1. All M is P
All M is S
∴ All S is P
2. All P is M
All M is S
∴ All S is P
3. All M is P
Some M is S
∴ Some S is P
4. All P is M
Some M is S
∴ Some S is P
5. All P is M
Some S is M
∴ Some S is P
6. All P is M
Some S is not M
∴ Some S is not P
7. All M is P
Some S is not M
∴ Some S is not P
8. All M is P
Some M is not S
∴ Some S is not P
9. No M is P
Some S is M
∴ Some S is not P
10. No P is M
Some S is M
∴ Some S is not P
11. No P is M
Some S is not M
∴ Some S is not P
12. No M is P
Some S is not M
∴ Some S is not P
13. No P is M
Some M is not S
∴ Some S is not P
14. No P is M
No M is S
∴ No S is P
15. No P is M
All M is S
∴ No S is P
16. No P is M
All S is M
∴ No S is P
17. All P is M
No S is M
∴ No S is P
18. All M is P
No S is M
∴ No S is P
19. Some M is P
Some M is not S
∴ Some S is not P
20. Some P is M
Some S is not M
∴ Some S is P













