In the last section, we introduced the four categorical forms. Those forms are below.
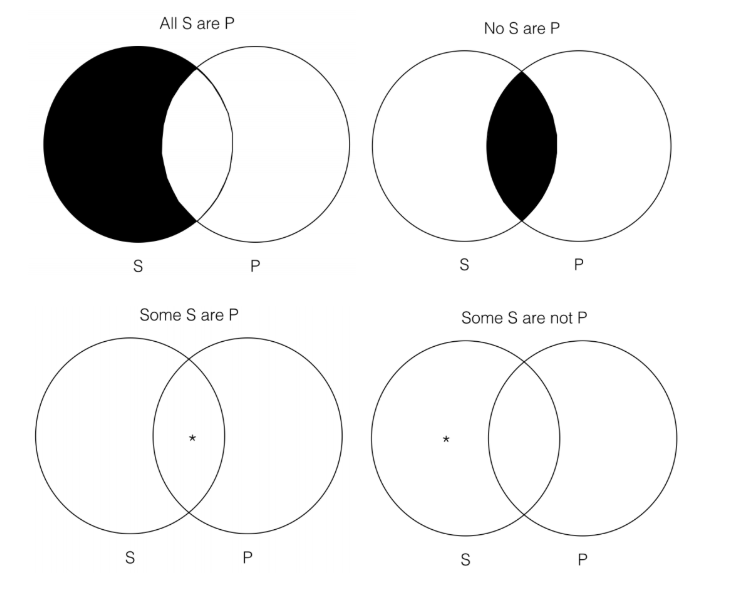
We can use Venn diagrams in order to determine whether certain kinds of arguments are valid or invalid. One such type of argument is what we will call “immediate categorical inferences.” An immediate categorical inference is simply an argument with one premise and one conclusion. For example:
- Some mammals are amphibious.
- Therefore, some amphibious things are mammals.
If we construct a Venn diagram for the premise and another Venn diagram for the conclusion, we will see that the Venn diagrams are identical to each other.
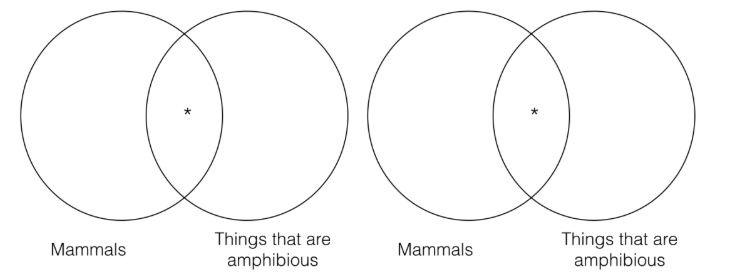
That is, the information that is represented in the Venn for the premise, is exactly the same information represented in the Venn for the conclusion. This argument passes the Venn test of validity because the conclusion Venn contains no additional information that is not already contained in the premise Venn. Thus, this argument is valid. Let’s now turn to an example of an invalid argument.
- All cars are vehicles.
- Therefore, all vehicles are cars.
Here are the Venns for the premise and the conclusion, respectively:
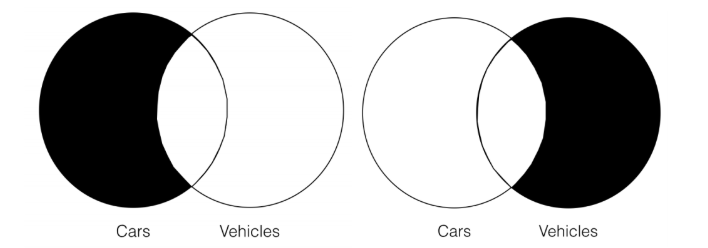
In this case, the Venns are clearly not the same. More importantly, we can see that the conclusion Venn (on the right) contains additional information that is not already contained in the premise Venn. In particular, the conclusion Venn allows that a) there could be things in the “car” category that aren’t in the “vehicle” category and b) that there cannot be anything in the “vehicle” category that isn’t also in the “car” category. That is not information that is contained in the premise Venn, which says that a) there isn’t anything in the category “car” that isn’t also in the category “vehicle” and b) that there could be things in the category “vehicle” that aren’t in the category “car.” Thus, this argument does not pass the Venn test of validity since there is information contained in the conclusion Venn that is not already contained in the premise Venn. Thus, this argument is invalid. The Venn test of validity is a formal method, because we can apply it even if we only know the form of the categorical statements, but don’t know what the categories referred to in the statements represent. For example, we can simply use “S” and “P” for the categories—and we clearly don’t know what these represent. For example:
- All S are P
- No P are S
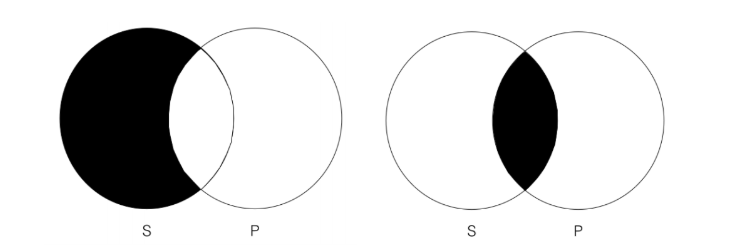
The conclusion (on the right) contains information that is not contained in the premise (on the left). In particular, the conclusion Venn explicitly rules out that there is anything that is both in the category “S” and in the category “P” while the premise Venn allows that this is the case (but does not require it). Thus, we can say that this argument fails the Venn test of validity and thus is invalid. We know this even though we have no idea what the categories “S” and “P” are. This is the mark of a formal method of evaluation.
Exercise
Apply the Venn test of validity in order to determine whether the following categorical inferences are valid or invalid.
1. All S are P; therefore, all P are S
2. Some S are P; therefore, some P are S
3. Some S are P; therefore, some P are not S
4. Some S are P; therefore, all P are S
5. No S are P; therefore, no P are S
6. No P are S; therefore, some S are P
7. Some S are not P; therefore, some P are not S
8. All S are P; therefore some P are not S






