2.4.12: Soundness

\(\def\Assign#1#2{ { #1^{\Struct{#2}} } }\)
\(\def\Atom#1#2{ { \mathord{#1}(#2) } }\)
\(\def\Bin{ {\mathbb{B}} }\)
\(\def\cardeq#1#2{ { #1 \approx #2 } }\)
\(\def\cardle#1#2{ { #1 \preceq #2 } }\)
\(\def\cardless#1#2{ { #1 \prec #2 } }\)
\(\def\cardneq#1#2{ { #1 \not\approx #2 } }\)
\(\def\comp#1#2{ { #2 \circ #1 } }\)
\(\def\concat{ { \;\frown\; } }\)
\(\def\Cut{ { \text{Cut} } }\)
\(\def\Discharge#1#2{ { [#1]^#2 } }\)
\(\def\DischargeRule#1#2{ { \RightLabel{#1}\LeftLabel{\scriptsize{#2} } } }\)
\(\def\dom#1{ {\operatorname{dom}(#1)} }\)
\(\def\Domain#1{ {\left| \Struct{#1} \right|} }\)
\(\def\Elim#1{ { {#1}\mathrm{Elim} } }\)
\(\newcommand{\Entails}{\vDash}\)
\(\newcommand{\EntailsN}{\nvDash}\)
\(\def\eq[#1][#2]{ { #1 = #2 } }\)
\(\def\eqN[#1][#2]{ { #1 \neq #2 } }\)
\(\def\equivclass#1#2{ { #1/_{#2} } }\)
\(\def\equivrep#1#2{ { [#1]_{#2} } }\)
\(\def\Exchange{ { \text{X} } }\)
\(\def\False{ { \mathbb{F} } }\)
\(\def\FalseCl{ { \lfalse_C } }\)
\(\def\FalseInt{ { \lfalse_I } }\)
\(\def\fCenter{ { \,\Sequent\, } }\)
\(\def\fdefined{ { \;\downarrow } }\)
\(\def\fn#1{ { \operatorname{#1} } }\)
\(\def\Frm[#1]{ {\operatorname{Frm}(\Lang #1)} }\)
\(\def\fundefined{ { \;\uparrow } }\)
\(\def\funimage#1#2{ { #1[#2] } }\)
\(\def\funrestrictionto#1#2{ { #1 \restriction_{#2} } }\)
\(\newcommand{\ident}{\equiv}\)
\(\newcommand{\indcase}[2]{#1 \ident #2\text{:}}\)
\(\newcommand{\indcaseA}[2]{#1 \text{ is atomic:}}\)
\(\def\indfrm{ { A } }\)
\(\def\indfrmp{ { A } }\)
\(\def\joinrel{\mathrel{\mkern-3mu}}\)
\(\def\lambd[#1][#2]{\lambda #1 . #2}\)
\(\def\Lang#1{ { \mathcal{#1} } }\)
\(\def\LeftR#1{ { {#1}\mathrm{L} } }\)
\(\def\len#1{ {\operatorname{len}(#1)} }\)
\(\def\lexists#1#2{ { \exists #1\, #2 } }\)
\(\def\lfalse{ {\bot} }\)
\(\def\lforall#1#2{ { \forall#1\, #2 } }\)
\(\newcommand{\lif}{\rightarrow}\)
\(\newcommand{\liff}{\leftrightarrow}\)
\(\def\Log#1{ { \mathbf{#1} } }\)
\(\def\ltrue{ {\top} }\)
\(\def\Id#1{ {\operatorname{Id}_#1} }\)
\(\def\Int{ {\mathbb{Z}} }\)
\(\def\Intro#1{ { {#1}\mathrm{Intro} } }\)
\(\def\mModel#1{ { \mathfrak{#1} } }\)
\(\newcommand{\mSat}[3][{}]{\mModel{#2}{#1}\Vdash{#3}}\)
\(\newcommand{\mSatN}[3][{}]{\mModel{#2}{#1}\nVdash{#3}}\)
\(\def\Nat{ {\mathbb{N}} }\)
\(\def\nicefrac#1#2{ {{}^#1/_#2} }\)
\(\def\num#1{ { \overline{#1} } }\)

\(\def\ran#1{ {\operatorname{ran}(#1)} }\)
\(\newcommand{\Obj}[1]{\mathsf{#1}}\)
\(\def\Rat{ {\mathbb{Q}} }\)
\(\def\Real{ {\mathbb{R}} }\)
\(\def\RightR#1{ { {#1}\mathrm{R} } }\)
\(\def\Part#1#2{ { \Atom{\Obj P}{#1, #2} } }\)
\(\def\pto{ { \hspace{0.1 cm}\to\hspace{-0.44 cm}\vcenter{\tiny{\hbox{|}}}\hspace{0.35 cm} } }\)
\(\def\PosInt{ {\mathbb{Z}^+} }\)
\(\def\Pow#1{ {\wp(#1)} }\)
\(\newcommand{\Proves}{\vdash}\)
\(\newcommand{\ProvesN}{\nvdash}\)
\(\def\Relbar{\mathrel{=}}\)
\(\newcommand{\Sat}[3][{}]{\Struct{#2}{#1}\vDash{#3}}\)
\(\newcommand{\SatN}[3][{}]{\Struct{#2}{#1}\nvDash{#3}}\)
\(\newcommand{\Sequent}{\Rightarrow}\)
\(\def\Setabs#1#2{ { \{#1:#2\} } }\)
\(\newcommand{\sFmla}[2]{#1\,#2}\)
\(\def\Struct#1{ {#1} }\)
\(\def\subst#1#2{ { #1/#2 } }\)
\(\def\Subst#1#2#3{ { #1[\subst{#2}{#3}] } }\)
\(\def\TMblank{ { 0 } }\)
\(\newcommand{\TMendtape}{\triangleright}\)
\(\def\TMleft{ { L } }\)
\(\def\TMright{ { R } }\)
\(\def\TMstay{ { N } }\)
\(\def\TMstroke{ { 1 } }\)
\(\def\TMtrans#1#2#3{ { #1,#2,#3 } }\)
\(\def\Trm[#1]{ {\operatorname{Trm}(\Lang #1)} }\)
\(\def\True{ { \mathbb{T} } }\)
\(\newcommand{\TRule}[2]{#2#1}\)
\(\def\tuple#1{ {\langle #1 \rangle} }\)
\(\newcommand{\Value}[3][\,]{\mathrm{Val}_{#1}^{#3}(#2)}\)
\(\def\Var{ { \mathrm{Var} } }\)
\(\newcommand{\varAssign}[3]{#1 \sim_{#3} #2}\)
\(\def\Weakening{ { \text{W} } }\)

A derivation system, such as the sequent calculus, is sound if it cannot derive things that do not actually hold. Soundness is thus a kind of guaranteed safety property for derivation systems. Depending on which proof theoretic property is in question, we would like to know for instance, that

1. every derivable \(A\) is valid;
2. if a sentence is derivable from some others, it is also a consequence of them;
3. if a set of sentences is inconsistent, it is unsatisfiable.

These are important properties of a derivation system. If any of them do not hold, the derivation system is deficient—it would derive too much. Consequently, establishing the soundness of a derivation system is of the utmost importance.

Because all these proof-theoretic properties are defined via derivability in the sequent calculus of certain sequents, proving (1)–(3) above requires proving something about the semantic properties of derivable sequents. We will first define what it means for a sequent to be valid, and then show that every derivable sequent is valid. (1)–(3) then follow as corollaries from this result.

Definition \(\PageIndex{1}\)

A structure \(\Struct M\) satisfies a sequent \(\Gamma \Sequent \Delta\) iff either \(\SatN{M}{A}\) for some \(A \in \Gamma\) or \(\Sat{M}{A}\) for some \(A \in \Delta\).

A sequent is valid iff every structure \(\Struct M\) satisfies it.

Theorem \(\PageIndex{1}\): Soundness

If \(\Log{LK}\) derives \(\Theta \Sequent \Xi\), then \(\Theta \Sequent \Xi\) is valid.

Proof. Let \(\pi\) be a derivation of \(\Theta \Sequent \Xi\). We proceed by induction on the number of inferences \(n\) in \(\pi\).

If the number of inferences is \(0\), then \(\pi\) consists only of an initial sequent. Every initial sequent \(A \Sequent A\) is obviously valid, since for every \(\Struct M\), either \(\SatN{M}{A}\) or \(\Sat{M}{A}\).

If the number of inferences is greater than 0, we distinguish cases according to the type of the lowermost inference. By induction hypothesis, we can assume that the premises of that inference are valid, since the number of inferences in the proof of any premise is smaller than \(n\).

First, we consider the possible inferences with only one premise.

1. The last inference is a weakening. Then \(\Theta \Sequent \Xi\) is either \(A, \Gamma \Sequent \Delta\) (if the last inference is \(\LeftR{\Weakening}\)) or \(\Gamma \Sequent \Delta, A\) (if it’s \(\RightR{\Weakening}\)), and the derivation ends in one of

   

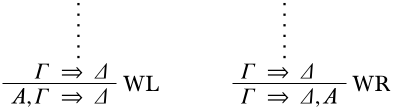
   By induction hypothesis, \(\Gamma \Sequent \Delta\) is valid, i.e., for every structure \(\Struct{M}\), either there is some \(C \in \Gamma\) such that \(\SatN{M}{C}\) or there is some \(C \in \Delta\) such that \(\Sat{M}{C}\).

   If \(\SatN{M}{C}\) for some \(C \in \Gamma\), then \(C \in \Theta\) as well since \(\Theta = A, \Gamma\), and so \(\SatN{M}{C}\) for some \(C \in \Theta\). Similarly, if \(\Sat{M}{C}\) for some \(C \in \Delta\), as \(C \in \Xi\), \(\Sat{M}{C}\) for some \(C \in \Xi\). Consequently, \(\Theta \Sequent \Xi\) is valid.

2. The last inference is \(\LeftR{\lnot}\): Then the premise of the last inference is \(\Gamma \Sequent \Delta, A\) and the conclusion is \(\lnot A, \Gamma \Sequent \Delta\), i.e., the derivation ends in

   

   and \(\Theta = \lnot A, \Gamma\) while \(\Xi = \Delta\).

   The induction hypothesis tells us that \(\Gamma \Sequent \Delta, A\) is valid, i.e., for every \(\Struct{M}\), either (a) for some \(C \in \Gamma\), \(\SatN{M}{C}\), or (b) for some \(C \in \Delta\), \(\Sat{M}{C}\), or (c) \(\Sat{M}{A}\). We want to show that \(\Theta \Sequent \Xi\) is also valid. Let \(\Struct{M}\) be a structure. If (a) holds, then there is \(C \in \Gamma\) so that \(\SatN{M}{C}\), but \(C \in \Theta\) as well. If (b) holds, there is \(C \in \Delta\) such that \(\Sat{M}{C}\), but \(C \in \Xi\) as well. Finally, if \(\Sat{M}{A}\), then \(\SatN{M}{\lnot A}\). Since \(\lnot A \in \Theta\), there is \(C \in \Theta\) such that \(\SatN{M}{C}\). Consequently, \(\Theta \Sequent \Xi\) is valid.

3. The last inference is \(\RightR{\lnot}\): Exercise.
4. The last inference is \(\LeftR{\land}\): There are two variants: \(A \land B\) may be inferred on the left from \(A\) or from \(B\) on the left side of the premise. In the first case, the \(\pi\) ends in

   

   and \(\Theta = A \land B, \Gamma\) while \(\Xi = \Delta\). Consider a structure \(\Struct M\). Since by induction hypothesis, \(A, \Gamma \Sequent \Delta\) is valid, (a) \(\SatN{M}{A}\), (b) \(\SatN{M}{C}\) for some \(C \in \Gamma\), or (c) \(\Sat{M}{C}\) for some \(C \in \Delta\). In case (a), \(\SatN{M}{A \land B}\), so there is \(C \in \Theta\) (namely, \(A \land B\)) such that \(\SatN{M}{C}\). In case (b), there is \(C \in \Gamma\) such that \(\SatN{M}{C}\), and \(C \in \Theta\) as well. In case (c), there is \(C \in \Delta\) such that \(\Sat{M}{C}\), and \(C \in \Xi\) as well since \(\Xi = \Delta\). So in each case, \(\Struct M\) satisfies \(A \land B, \Gamma \Sequent \Delta\). Since \(\Struct{M}\) was arbitrary, \(\Gamma \Sequent \Delta\) is valid. The case where \(A \land B\) is inferred from \(B\) is handled the same, changing \(A\) to \(B\).

5. The last inference is \(\RightR{\lor}\): There are two variants: \(A \lor B\) may be inferred on the right from \(A\) or from \(B\) on the right side of the premise. In the first case, \(\pi\) ends in

   

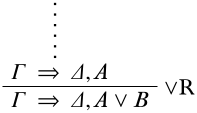
   Now \(\Theta = \Gamma\) and \(\Xi = \Delta, A \lor B\). Consider a structure \(\Struct{M}\). Since \(\Gamma \Sequent \Delta, A\) is valid, (a) \(\Sat{M}{A}\), (b) \(\SatN{M}{C}\) for some \(C \in \Gamma\), or (c) \(\Sat{M}{C}\) for some \(C \in \Delta\). In case (a), \(\Sat{M}{A \lor B}\). In case (b), there is \(C \in \Gamma\) such that \(\SatN{M}{C}\). In case (c), there is \(C \in \Delta\) such that \(\Sat{M}{C}\). So in each case, \(\Struct{M}\) satisfies \(\Gamma \Sequent \Delta, A \lor B\), i.e., \(\Theta \Sequent \Xi\). Since \(\Struct{M}\) was arbitrary, \(\Theta \Sequent \Xi\) is valid. The case where \(A \lor B\) is inferred from \(B\) is handled the same, changing \(A\) to \(B\).

6. The last inference is \(\RightR{\lif}\): Then \(\pi\) ends in

   

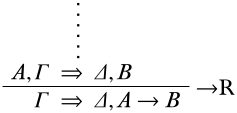
   Again, the induction hypothesis says that the premise is valid; we want to show that the conclusion is valid as well. Let \(\Struct{M}\) be arbitrary. Since \(A, \Gamma \Sequent \Delta, B\) is valid, at least one of the following cases obtains: (a) \(\SatN{M}{A}\), (b) \(\Sat{M}{B}\), (c) \(\SatN{M}{C}\) for some \(~C \in \Gamma\), or (d) \(\Sat{M}{C}\) for some \(C \in \Delta\). In cases (a) and (b), \(\Sat{M}{A \lif B}\) and so there is a \(C \in \Delta, A \lif B\) such that \(\Sat{M}{C}\). In case (c), for some \(C \in \Gamma\), \(\SatN{M}{C}\). In case (d), for some \(C \in \Delta\), \(\Sat{M}{C}\). In each case, \(\Struct{M}\) satisfies \(\Gamma \Sequent \Delta, A \lif B\). Since \(\Struct{M}\) was arbitrary, \(\Gamma \Sequent \Delta, A \lif B\) is valid.

7. The last inference is \(\LeftR{\lforall{}{}}\): Then there is a formula \(A(x)\) and a closed term \(t\) such that \(\pi\) ends in

   

   We want to show that the conclusion \(\lforall{x}{A(x)}, \Gamma \Sequent \Delta\) is valid. Consider a structure \(\Struct M\). Since the premise \(A(t), \Gamma \Sequent \Delta\) is valid, (a) \(\SatN{M}{A(t)}\), (b) \(\SatN{M}{C}\) for some \(C \in \Gamma\), or (c) \(\Sat{M}{C}\) for some \(C \in \Delta\). In case (a), by Proposition 5.14.4, if \(\Sat{M}{\lforall{x}{A(x)}}\), then \(\Sat{M}{A(t)}\). Since \(\SatN{M}{A(t)}\), \(\SatN{M}{\lforall{x}{A(x)}}\). In case (b) and (c), \(\Struct{M}\) also satisfies \(\lforall{x}{A(x)}, \Gamma \Sequent \Delta\). Since \(\Struct M\) was arbitrary, \(\lforall{x}{A(x)}, \Gamma \Sequent \Delta\) is valid.

8. The last inference is \(\RightR{\lexists{}{}}\): Exercise.
9. The last inference is \(\RightR{\lforall{}{}}\): Then there is a formula \(A(x)\) and a constant symbol \(a\) such that \(\pi\) ends in

   

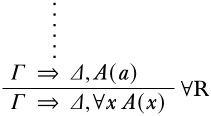
   where the eigenvariable condition is satisfied, i.e., \(a\) does not occur in \(A(x)\), \(\Gamma\), or \(\Delta\). By induction hypothesis, the premise of the last inference is valid. We have to show that the conclusion is valid as well, i.e., that for any structure \(\Struct M\), (a) \(\Sat{M}{\lforall{x}{A(x)}}\), (b) \(\SatN{M}{C}\) for some \(C \in \Gamma\), or (c) \(\Sat{M}{C}\) for some \(C \in \Delta\).

   Suppose \(\Struct{M}\) is an arbitrary structure. If (b) or (c) holds, we are done, so suppose neither holds: for all \(C \in \Gamma\), \(\Sat{M}{C}\), and for all \(C \in \Delta\), \(\SatN{M}{C}\). We have to show that (a) holds, i.e., \(\Sat{M}{\lforall{x}{A(x)}}\). By Proposition 5.12.4, if suffices to show that \(\Sat[,s]{M}{A(x)}\) for all variable assignments \(s\). So let \(s\) be an arbitrary variable assignment. Consider the structure \(\Struct{M'}\) which is just like \(\Struct{M}\) except \(\Assign{a}{M'} = s(x)\). By Corollary 5.13.1, for any \(C \in \Gamma\), \(\Sat{M'}{C}\) since \(a\) does not occur in \(\Gamma\), and for any \(C \in \Delta\), \(\SatN{M'}{C}\). But the premise is valid, so \(\Sat{M'}{A(a)}\). By Proposition 5.12.3, \(\Sat[,s]{M'}{A(a)}\), since \(A(a)\) is a sentence. Now \(\varAssign{s}{s}{x}\) with \(s(x) = \Value[s]{a}{M'}\), since we’ve defined \(\Struct{M'}\) in just this way. So Proposition 5.13.3 applies, and we get \(\Sat[,s]{M'}{A(x)}\). Since \(a\) does not occur in \(A(x)\), by Proposition 5.13.1, \(\Sat[,s]{M}{A(x)}\). Since \(s\) was arbitrary, we’ve completed the proof that \(\Sat[,s]{M}{A(x)}\) for all variable assignments.

10. The last inference is \(\LeftR{\lexists{}{}}\): Exercise.

Now let’s consider the possible inferences with two premises.

1. The last inference is a cut: then \(\pi\) ends in

   

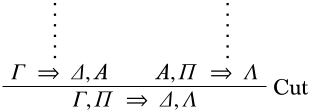
   Let \(\Struct{M}\) be a structure. By induction hypothesis, the premises are valid, so \(\Struct{M}\) satisfies both premises. We distinguish two cases: (a) \(\SatN{M}{A}\) and (b) \(\Sat{M}{A}\). In case (a), in order for \(\Struct{M}\) to satisfy the left premise, it must satisfy \(\Gamma \Sequent \Delta\). But then it also satisfies the conclusion. In case (b), in order for \(\Struct{M}\) to satisfy the right premise, it must satisfy \(\Pi \setminus \Lambda\). Again, \(\Struct{M}\) satisfies the conclusion.

2. The last inference is \(\RightR{\land}\). Then \(\pi\) ends in

   

   Consider a structure \(\Struct M\). If \(\Struct{M}\) satisfies \(\Gamma \Sequent \Delta\), we are done. So suppose it doesn’t. Since \(\Gamma \fCenter \Delta, A\) is valid by induction hypothesis, \(\Sat{M}{A}\). Similarly, since \(\Gamma \Sequent \Delta, B\) is valid, \(\Sat{M}{B}\). But then \(\Sat{M}{A \land B}\).

3. The last inference is \(\LeftR{\lor}\): Exercise.
4. The last inference is \(\LeftR{\lif}\). Then \(\pi\) ends in

   

   Again, consider a structure \(\Struct{M}\) and suppose \(\Struct{M}\) doesn’t satisfy \(\Gamma, \Pi \Sequent \Delta, \Lambda\). We have to show that \(\SatN{M}{A \lif B}\). If \(\Struct{M}\) doesn’t satisfy \(\Gamma, \Pi \Sequent \Delta, \Lambda\), it satisfies neither \(\Gamma \Sequent \Delta\) nor \(\Pi \Sequent \Lambda\). Since, \(\Gamma \Sequent \Delta, A\) is valid, we have \(\Sat{M}{A}\). Since \(B, \Pi \Sequent \Lambda\) is valid, we have \(\SatN{M}{B}\). But then \(\SatN{M}{A \lif B}\), which is what we wanted to show.

◻

Problem \(\PageIndex{1}\)

Complete the proof of Theorem \(\PageIndex{1}\).

Corollary \(\PageIndex{1}\)

If \(\Proves A\) then \(A\) is valid.

Corollary \(\PageIndex{2}\)

If \(\Gamma \Proves A\) then \(\Gamma \Entails A\).

Proof. If \(\Gamma \Proves A\) then for some finite subset \(\Gamma_0 \subseteq \Gamma\), there is a derivation of \(\Gamma_0 \Sequent A\). By Theorem \(\PageIndex{1}\), every structure \(\Struct{M}\) either makes some \(B \in \Gamma_0\) false or makes \(A\) true. Hence, if \(\Sat{M}{\Gamma}\) then also \(\Sat{M}{A}\). ◻

Corollary \(\PageIndex{3}\)

If \(\Gamma\) is satisfiable, then it is consistent.

Proof. We prove the contrapositive. Suppose that \(\Gamma\) is not consistent. Then there is a finite \(\Gamma_0 \subseteq \Gamma\) and a derivation of \(\Gamma_0 \Sequent \quad\). By Theorem \(\PageIndex{1}\), \(\Gamma_0 \Sequent \quad\) is valid. In other words, for every structure \(\Struct{M}\), there is \(C \in \Gamma_0\) so that \(\SatN{M}{C}\), and since \(\Gamma_0 \subseteq \Gamma\), that \(C\) is also in \(\Gamma\). Thus, no \(\Struct{M}\) satisfies \(\Gamma\), and \(\Gamma\) is not satisfiable. ◻