4.5: Testing the Validity of Sentential Logic
- Page ID
- 24338
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Having dealt with the task of taming natural language, we are finally in a position to complete the second and third steps of building a logic: defining logical form and developing a test for validity. The test will involve applying skills that we’ve already learned: setting up truth tables and computing the truth-values of compounds. First, we must define logical form in SL.
Logical Form in SL
This will seem trivial, but it is necessary. We’re learning how to evaluate arguments expressed in SL. Like any evaluation of deductive arguments, the outcome hinges on the argument’s form. So what is the form of an SL argument? Let’s consider an example; here is an argument in SL:
A ⊃ B
~B
Therefore, ~ A
‘A’ and ‘B’ stand for simple sentences in English; we don’t care which ones. We’re working within SL: given an argument in this language, how do we determine its form? Quite simply, by systematically replacing capital letters with variables (lower-case letters like ‘p’, ‘q’, and ‘r’). The form of that particular SL argument is this:
p ⊃ q
~q
Therefore, ~ p
The replacement of capital letters with lower-case variables was systematic in this sense: each occurrence of the same capital letter (e.g., ‘A’) was replaced with the same variable (e.g., ‘p’).
To generate the logical form of an SL argument, what we do is systematically replace SL sentences with what we’ll call sentence-forms. An SL sentence is just a well-formed combination of SL symbols—capital letters, operators, and parentheses. A sentence-form is a combination of symbols that would be well-formed in SL, except that it has lower-case variables instead of capital letters.
Again, this may seem like a trivial change, but it is necessary. Remember, when we’re testing an argument for validity, we’re checking to see whether its form is such that it’s possible for its premises to turn out true and its conclusion false. This means checking various ways of filling in the form with particular sentences. Variables—as the name suggests—can vary in the way we need: they are generic and can be replaced with any old particular sentence. Actual SL constructions feature capital letters, which are actual sentences having specific truth-values. It is conceptually incoherent to speak of checking different possibilities for actual sentences. So we must switch to sentence-forms.
The Truth Table Test for Validity
To test an SL argument for validity, we identify its logical form, then create a truth table with columns for each of the variables and sentence-forms in the argument’s form. Filling in columns of Ts and Fs under each of the operators in those sentence-forms will allow us to check for what we’re looking for: an instance of the argument’s form for which the premises turn out true and the conclusion turns out false. Finding such an instance demonstrates the argument’s invalidity, while failing to find one demonstrates its validity.
To see how this works, it will be useful to work through an example. Consider the following argument in English:
If Democrats take back Congress, lots of new laws will be passed.
Democrats won’t take back Congress.
Therefore, lots of new laws won’t be passed.
We’ll evaluate it by first translating it into SL. Let ‘D’ stand for ‘Democrats take back Congress’ and ‘L’ stand for ‘Lots of new laws will be passed’. This is the argument in SL:
D ⊃ L
~D
Therefore, ~ L
First, the logical form. Replacing ‘D’ with ‘p’ and ‘L’ with ‘q’, we get:
p ⊃ q
~p
Therefore, ~ q
Now we set up a truth table, with columns for each of the variables and columns for each of the sentence-forms. To determine how many rows our table needs, we note the number of different variables that occur in the argument-form (call that number ‘n’); the table will need 2n rows. In this case, we have two variables—‘p’ and ‘q’—and so we need 22 = 4 rows. (If there were three variables, we would need 23 = 8 rows; if there were four, 24 = 16; and so on.) Here is the table we need to fill in for this example:
First, we fill in the “base columns”. These are the columns for the variables. We do this systematically. Start with the right-most column (under ‘q’ in this case), and fill in Ts and Fs alternately: T, F, T, F, T, F, ... as many times as you need—until you’ve got a truth-value in every row. That gives us this:
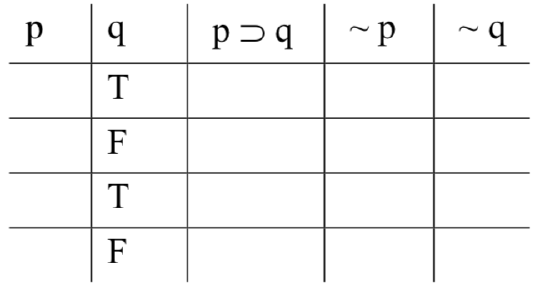
Next, we move to the base column to the left of the one we just filled in (under ‘p’ now), and fill in Ts and Fs by alternating in twos: T, T, F, F, T, T, F, F,... as many times as we need. The result is this:
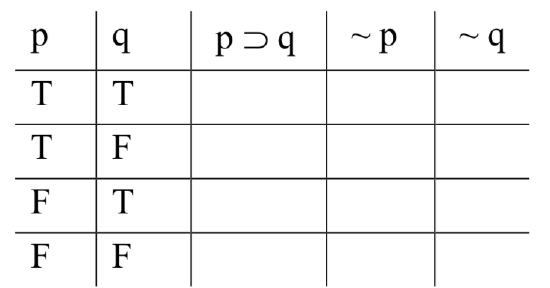
If there were a third base column, we would fill in the Ts and Fs by alternating in fours: T, T, T, T, F, F, F, F.... For a fourth base column, we would alternate every other eight. And so on.
Next, we need to fill in columns of Ts and Fs under each of the operators in the statement-forms’ columns. To do this, we apply our knowledge of how to compute the truth-values of compounds in terms of the values of their components, consulting the operators’ truth table definitions. We know how to compute the values of p ⊃ q: it’s false when p is true and q false; true otherwise. We know how to compute the values of ~ p and ~ q: those are just the opposites of the values of p and q in each of the rows. Making these computations, we fill the table in thus:
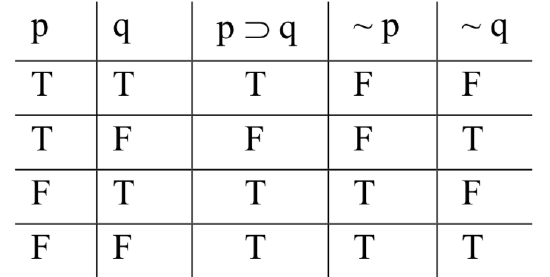
Once the table is filled in, we check to see if we have a valid or invalid form. The mark of an invalid form is that it’s possible for the premises to be true and the conclusion false. Here, the rows of the table are the possibilities—the four possible outcomes of plugging in particular SL sentences for the variables: both true; the first is true, but the second false; the first false but the second true; both false. The reason we systematically fill in the base columns as described above is that the method ensures that our rows will collectively exhaust all these possible combinations.
So, to see if it’s possible for the premises to come out true and the conclusion to come out false, we check each of the rows, looking for one in which this happens—one in which there’s a T under ‘p ⊃ q’, a T under ‘~ p’, and an F under ‘~ q’. And we have one: in row 3, the premises come out true and the conclusion comes out false. This is enough to show that the argument is invalid:
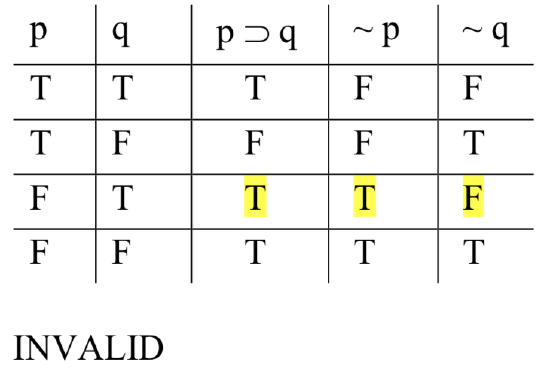
When we’re checking for validity, we’re looking for one thing, and one thing only: a row (or rows) in which the premises come out true and the conclusion comes out false. If we find one, we have shown that the argument is invalid. If we don’t find one, that indicates that it’s impossible for the premises to be true and the conclusion false—and so the argument is valid. Either way, the only thing we look for is a row with true premises and a false conclusion. Every other kind of row is irrelevant. It’s common for beginners to mistakenly think they are. The fourth row in the table above, for example, looks significant. Everything comes out true in that row. Doesn’t that mean something—something good, like that the argument’s valid? No. Remember, each row represents a possibility; what row 4 shows is that it’s possible for the premises to be true and the conclusion true. But that’s not enough for validity. For an argument to be valid, the premises must guarantee the conclusion; whenever they’re true, the conclusion must be true. That it’s merely possible that they all come out true is not enough.
Let’s look at a more involved example, to see how the computation of the truth-values of the statement-forms must sometimes proceed in stages. The skill required here is nothing new—it’s just identifying main operators and computing the values of the simplest components first—but it takes careful attention to keep everything straight. Consider this SL argument (never mind what its English counterpart is):
(~ A • B) ∨ ~ X
B ⊃ A
Therefore, ~ X
To get its form, we replace ‘A’ with ‘p’, ‘B’ with ‘q’, and ‘X’ with ‘r’:
(~ p • q) ∨ ~ r
q ⊃ p
Therefore, ~ r
So our truth-table will look like this (eight rows because we have three variables; 23 = 8):

Filling in the base columns as prescribed above—alternating every other one for the column under ‘r’, every two under ‘q’, and every four under ‘p’—we get:
Now we turn our attention to the three sentence-forms. We’ll start with the first premise, the compound ‘(~ p • q) ∨ ~ r’. We need to compute the truth-value of this formula. We know how to do this, provided we have the truth-values of the simplest parts; we’ve solved problems like that already. The only difference in the case of truth tables is that there are multiple different assignments of truth-values to the simplest parts. In this case, there are eight different ways of assigning truth-values to ‘p’, ‘q’, and ‘r’; those are represented by the eight different rows of the table. So we’re solving a problem we know how to solve; we’re just doing it eight times.
We start by identifying the main operator of the compound formula. In this case, it’s the wedge: we have a disjunction; the left-hand disjunct is ‘(~ p • q)’, and the right-hand disjunct is ‘~ r’. To figure out what happens under the wedge in our table, we must first figure out the values of these components. Both disjuncts are themselves compound: ‘(~ p • q)’ is a conjunction, and ‘~ r’ is a negation. Let’s tackle the conjunction first. To figure out what happens under the dot, we need to know the values of ‘~ p’ and ‘q’. We know the values of ‘q’; that’s one of the base columns. We must compute the value of ‘~ p’. That’s easy: in each row, the value of ‘~ p’ will just be the opposite of the value of ‘p’. We note the values under the tilde, the operator that generates them:
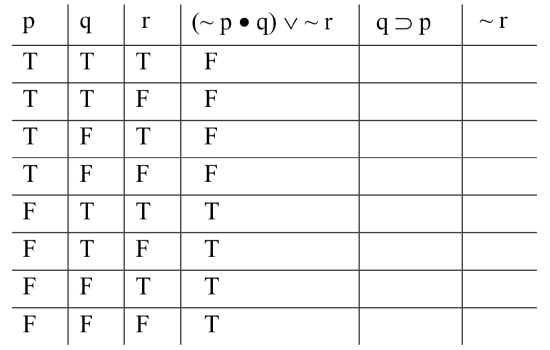
To compute the value of the conjunction, we consider the result, in each row, of the truth-function for dot, where the inputs are the value under the tilde in ‘~ p’ and the value under ‘q’ in the base column. In rows 1 and 2, it’s F • T; in rows 3 and 4, F • F; and so on. The results:
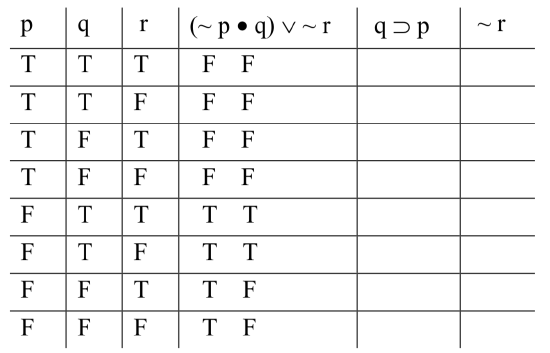
The column we just produced, under the dot, gives us the range of truth-values for the left-hand disjunct in the first premise. We need the values of the right-hand disjunct. That’s just ‘~ r’, which is easy to compute: it’s just the opposite value of ‘r’ in every row:

Now we can finally determine the truth-values for the whole disjunction. We compute the value of the wedge’s truth-function, where the inputs are the columns under the dot, on the one hand, and the tilde from ‘~ r’ on the other. F ∨ F, F ∨ T, F ∨ F, and so on:
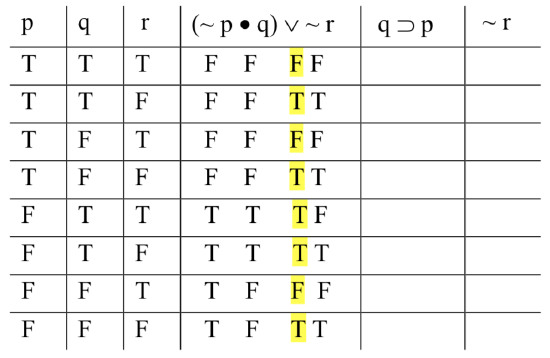
Since that column represents the range of possible values for the entire sentence-form, we highlight it. When we test for validity, we’re looking for rows where the premises as a whole come out true; we’ll be looking for the value under their main operators. To make that easier, just so we don’t lose track of things visually because of all those columns, we highlight the one under the main operator.
Next, the second premise, which is thankfully much less complex. It is, however, slightly tricky. We need to compute the value of a conditional here. But notice that things are a bit different than usual: the antecedent, ‘q’, has its base column to the right of the column for the consequent, ‘p’. That’s a bit awkward. We’re used to computing conditionals from left-to-right; we’ll have to mentally adjust to the fact that ‘q ⊃ p’ goes from right-to-left. (Alternatively, if it helps, you can simply reproduce the base columns underneath the variables in the ‘q ⊃ p’ column.) So in the first two rows, we compute T ⊃ T; but in rows 3 and 4, it’s F ⊃ T; in rows 5 and 6, it’s T ⊃ F (the only circumstance in which conditionals turn out false); an in rows 7 and 8, it’s F ⊃ F. Here is the result:
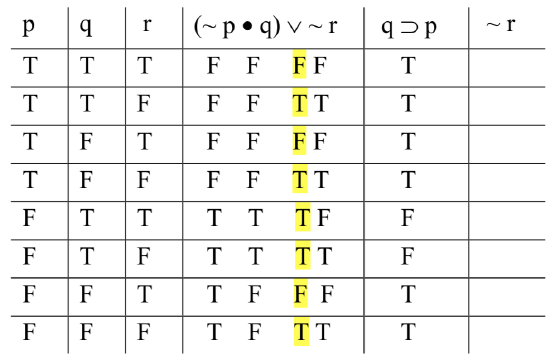
No need to highlight that column, as it’s the only one we produced for that premise, so there can be no confusion.
We finish the table by computing the values for the conclusion, which is easy:

Is the argument valid? We look for a row with true premises and a false conclusion. There are none. The only two rows in which both premises come out true are the second and the eighth, and in both we also have a true conclusion. It is impossible for the premises to be true and the conclusion false, so the argument is valid.
So that is how we test arguments for validity in SL. It’s a straightforward procedure; the main source of error is simple carelessness. Go step by step, keep careful track of what you’re doing, and it should be easy. It’s worth noting that the truth table test is what logicians call a “decision procedure”: it’s a rule-governed process (an algorithm) that is guaranteed to answer your question (in this case: valid or invalid?) in a finite number of steps. It is possible to program a computer to run the truth table test on arbitrarily long SL arguments. This is comforting, since once one gets more than four variables or so, the process becomes unwieldy.
Exercises
Test the following arguments for validity. For those that are invalid, specify the row(s) that demonstrate the invalidity.
1. ~ A, therefore ~ A ∨ B
2. A ⊃ B, ~ B, therefore ~ A
3. A ∨ B, ~ A, therefore ~ B
4. ~ (A ≡ B), A ∨ B, therefore A • B
5. ~ (A ⊃ B), ~ B ∨ ~ A, therefore ~ (~ A ≡ B)
6. ~ B ∨ A, ~ A, A ≡ B, therefore ~ B
7. A ⊃ (B • C), ~ B ∨ ~ C, therefore ~ A
8. ~ A ∨ C, ~ B ⊃ ~ C, therefore A ≡ C
9. ~ A ∨ (~ B • C), ~ (C ∨ B) ⊃ A, therefore ~ C ⊃ ~ B
10. A ∨ B, B ⊃ C, ~ C, therefore ~ A


