1.5: Diagramming Arguments
- Page ID
- 24317
Before we get down to the business of evaluating arguments—of judging them valid or invalid, strong or weak—we still need to do some preliminary work. We need to develop our analytical skills to gain a deeper understanding of how arguments are constructed, how they hang together. So far, we’ve said that the premises are there to support the conclusion. But we’ve done very little in the way of analyzing the structure of arguments: we’ve just separated the premises from the conclusion. We know that the premises are supposed to support the conclusion. What we haven’t explored is the question of just how the premises in a given argument do that job—how they work together to support the conclusion, what kinds of relationships they have with one another. This is a deeper level of analysis than merely distinguishing the premises from the conclusion; it will require a mode of presentation more elaborate than a list of propositions with the bottom one separated from the others by a horizontal line. To display our understanding of the relationships among premises supporting the conclusion, we are going to depict them: we are going to draw diagrams of arguments.
Here’s how the diagrams will work. They will consist of three elements: (1) circles with numbers inside them—each of the propositions in the argument we’re diagramming will be assigned a number, so these circled numbers in the diagram will represent the propositions; (2) arrows pointed at circled numbers—these will represent relationships of support, where one or more propositions provide a reason for believing the one pointed to; and (3) horizontal brackets—propositions connected by these will be interdependent (in a sense to be specified below).
Our diagrams will always feature the circled number corresponding to the conclusion at the bottom. The premises will be above, with brackets and arrows indicating how they collectively support the conclusion and how they’re related to one another. There are a number of different relationships that premises can have to one another. We will learn how to draw diagrams of arguments by considering them in turn.
Independent Premises
Often, different premises will support a conclusion—or another premise—individually, without help from any others. When this is the case, we draw an arrow from the circled number representing that premise to the circled number representing the proposition it supports.
Consider this simple argument:
① Marijuana is less addictive than alcohol. In addition, ② it can be used as a medicine to treat a variety of conditions. Therefore, ③ marijuana should be legal.
The last proposition is clearly the conclusion (the word ‘therefore’ is a big clue), and the first two propositions are the premises supporting it. They support the conclusion independently. The mark of independence is this: each of the premises would still provide support for the conclusion even if the other weren’t true; each, on its own, gives you a reason for believing the conclusion. In this case, then, we diagram the argument as follows:

Intermediate Premises
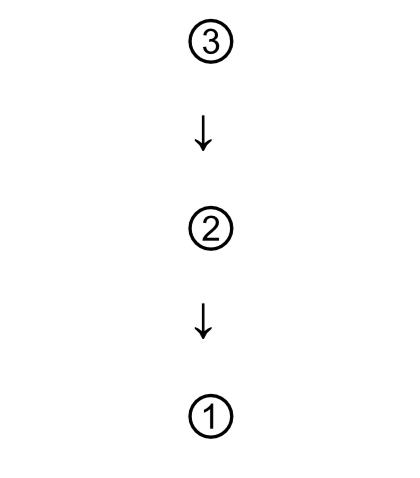
Some premises support their conclusions more directly than others. Premises provide more indirect support for a conclusion by providing a reason to believe another premise that supports the conclusion more directly. That is, some premises are intermediate between the conclusion and other premises.
Consider this simple argument:
① Automatic weapons should be illegal. ② They can be used to kill large numbers of people in a short amount of time. This is because ③ all you have to do is hold down the trigger and bullets come flying out in rapid succession.
The conclusion of this argument is the first proposition, so the premises are propositions 2 and 3. Notice, though, that there’s a relationship between those two claims. The third sentence starts with the phrase ‘This is because’, indicating that it provides a reason for another claim. The other claim is proposition 2; ‘This’ refers to the claim that automatic weapons can kill large numbers of people quickly. Why should I believe that they can do that? Because all one has to do is hold down the trigger to release lots of bullets really fast. Proposition 2 provides immediate support for the conclusion (automatic weapons can kill lots of people really quickly, so we should make them illegal); proposition 3 supports the conclusion more indirectly, by giving support to proposition 2. Here is how we diagram in this case:
Joint Premises
Sometimes premises need each other: the job of supporting another proposition can’t be done by each on its own; they can only provide support together, jointly. Far from being independent, such premises are interdependent. In this situation, on our diagrams, we join together the interdependent premises with a bracket underneath their circled numbers.
There are a number of different ways in which premises can provide joint support. Sometimes, premises just fit together like a hand in a glove; or, switching metaphors, one premise is like the key that fits into the other to unlock the proposition they jointly support. An example can make this clear:
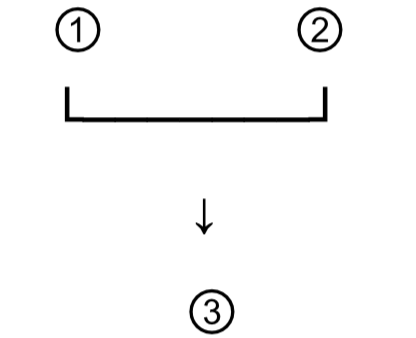
① The chef has decided that either salmon or chicken will be tonight’s special. ② Salmon won’t be the special. Therefore, ③ the special will be chicken.
Neither premise 1 nor premise 2 can support the conclusion on its own. A useful rule of thumb for checking whether one proposition can support another is this: read the first proposition, then say the word ‘therefore’, then read the second proposition; if it doesn’t make any sense, then you can’t draw an arrow from the one to the other. Let’s try it here: “The chef has decided that either salmon or chicken will be tonight’s special; therefore, the special will be chicken.” That doesn’t make any sense. What happened to salmon? Proposition 1 can’t support the conclusion on its own. Neither can the second: “Salmon won’t be the special; therefore, the special will be chicken.” Again, that makes no sense. Why chicken? What about steak, or lobster? The second proposition can’t support the conclusion on its own, either; it needs help from the first proposition, which tells us that if it’s not salmon, it’s chicken. Propositions 1 and 2 need each other; they support the conclusion jointly. This is how we diagram the argument:
The same diagram would depict the following argument:
① John Le Carre gives us realistic, three-dimensional characters and complex, interesting plots. ② Ian Fleming, on the other hand, presents an unrealistically glamorous picture of international espionage, and his plotting isn’t what you’d call immersive. ③ Le Carre is a better author of spy novels than Fleming.
In this example, the premises work jointly in a different way than in the previous example. Rather than fitting together hand-in-glove, these premises each give us half of what we need to arrive at the conclusion. The conclusion is a comparison between two authors. Each of the premises makes claims about one of the two authors. Neither one, on its own, can support the comparison, because the comparison is a claim about both of them. The premises can only support the conclusion together. We would diagram this argument the same way as the last one.
Another common pattern for joint premises is when general propositions need help to provide support for particular propositions. Consider the following argument:
① People shouldn’t vote for racist, incompetent candidates for president. ② Donald Trump seems to make a new racist remark at least twice a week. And ③ he lacks the competence to run even his own (failed) businesses, let alone the whole country. ④ You shouldn’t vote for Trump to be the president.
The conclusion of the argument, the thing it’s trying to convince us of, is the last proposition—you shouldn’t vote for Trump. This is a particular claim: it’s a claim about an individual person, Trump. The first proposition in the argument, on the other hand, is a general claim: it asserts that, generally speaking, people shouldn’t vote for incompetent racists; it makes no mention of an individual candidate. It cannot, therefore, support the particular conclusion—about Trump—on its own. It needs help from other particular claims—propositions 2 and 3—that tell us that the individual in the conclusion, Trump, meets the conditions laid out in the general proposition 1: racism and incompetence. This is how we diagram the argument:

Occasionally, an argumentative passage will only explicitly state one of a set of joint premises because the others “go without saying”—they are part of the body of background information about which both speaker and audience agree. In the last example, that Trump was an incompetent racist was not uncontroversial background information. But consider this argument:
① It would be good for the country to have a woman with lots of experience in public office as president. ② People should vote for Hillary Clinton.
Diagramming this argument seems straightforward: an arrow pointing from 1 to 2. But we’ve got the same relationship between the premise and conclusion as in the last example: the premise is a general claim, mentioning no individual at all, while the conclusion is a particular claim about Hillary Clinton. Doesn’t the general premise “need help” from particular claims to the effect that the individual in question, Hillary Clinton, meets the conditions set forth in the premise—i.e., that she’s a woman and that she has lots of experience in public office? No, not really. Everybody knows those things about her already; they go without saying, and can therefore be left unstated (implicit, tacit).
But suppose we had included those obvious truths about Clinton in our presentation of the argument; suppose we had made the tacit premises explicit:
① It would be good for the country to have a woman with lots of experience in public office as president. ② Hillary Clinton is a woman. And ③ she has deep experience with public offices—as a First Lady, U.S. Senator, and Secretary of State. ④ People should vote for Hillary Clinton.
How do we diagram this? Earlier, we talked about a rule of thumb for determining whether or not it’s a good idea to draw an arrow from one number to another in a diagram: read the sentence corresponding to the first number, say the word ‘therefore’, then read the sentence corresponding to the second number; if it doesn’t make sense, then the arrow is a bad idea. But if it does make sense, does that mean you should draw the arrow? Not necessarily. Consider the first and last sentences in this passage. Read the first, then ‘therefore’, then the last. Makes pretty good sense! That’s just the original formulation of the argument with the tacit propositions remaining implicit. And in that case we said it would be OK to draw an arrow from the general premise’s number straight to the conclusion’s. But when we add the tacit premises—the second and third sentences in this passage—we can’t draw an arrow directly from ① to ④. To do so would obscure the relationship among the first three propositions and misrepresent how the argument works. If we drew an arrow from ① to ④, what would we do with ② to ③ in our diagram? Do they get their own arrows, too? No, that won’t do. Such a diagram would be telling us that the first three propositions each independently provide a reason for the conclusion. But they’re clearly not independent; there’s a relationship among them that our diagram must capture, and it’s the same relationship we saw in the parallel argument about Trump, with the particular claims in the second and third propositions working together with the general claim in the first:

The arguments we’ve looked at thus far have been quite short—only two or three premises. But of course some arguments are longer than that. Some are much longer. It may prove instructive, at this point, to tackle one of these longer bits of reasoning. It comes from the (fictional) master of analytical deductive reasoning, Sherlock Holmes. The following passage is from the first Holmes story—A Study in Scarlet, one of the few novels Arthur Conan Doyle wrote about his most famous character—and it’s a bit of early dialogue that takes place shortly after Holmes and his longtime associate Dr. Watson meet for the first time. At that first meeting, Holmes did his typical Holmes-y thing, where he takes a quick glance at a person and then immediately makes some startling inference about them, stating some fact about them that it seems impossible he could have known. Here they are—Holmes and Watson—talking about it a day or two later. Holmes is the first to speak:
“Observation with me is second nature. You appeared to be surprised when I told you, on our first meeting, that you had come from Afghanistan.”
“You were told, no doubt.”
“Nothing of the sort. I knew you came from Afghanistan. From long habit the train of thoughts ran so swiftly through my mind, that I arrived at the conclusion without being conscious of intermediate steps. There were such steps, however. The train of reasoning ran, ‘Here is a gentleman of a medical type, but with the air of a military man. Clearly an army doctor, then. He has just come from the tropics, for his face is dark, and that is not the natural tint of his skin, for his wrists are fair. He has undergone hardship and sickness, as his haggard face says clearly. His left arm has been injured. He holds it in a stiff and unnatural manner. Where in the tropics could an English army doctor have seen much hardship and got his arm wounded? Clearly in Afghanistan.’ The whole train of thought did not occupy a second. I then remarked that you came from Afghanistan, and you were astonished.” (Also excerpted in Copi and Cohen, 2009, Introduction to Logic 13e, pp. 58 - 59.)
This is an extended inference, with lots of propositions leading to the conclusion that Watson had been in Afghanistan. Before we draw the diagram, let’s number the propositions involved in the argument:
- Watson was in Afghanistan.
- Watson is a medical man.
- Watson is a military man.
- Watson is an army doctor.
- Watson has just come from the tropics.
- Watson’s face is dark.
- Watson’s skin is not naturally dark.
- Watson’s wrists are fair.
- Watson has undergone hardship and sickness.
- Watson’s face is haggard.
- Watson’s arm has been injured.
- Watson holds his arm stiffly and unnaturally.
- Only in Afghanistan could an English army doctor have been in the tropics, seen much hardship and got his arm wounded.
Lots of propositions, but they’re mostly straightforward, right from the text. We just had to do a bit of paraphrasing on the last one—Holmes asks a rhetorical question and answers it, the upshot of which is the general proposition in 13. We know that proposition 1 is our conclusion, so that goes at the bottom of the diagram. The best thing to do is to start there and work our way up. Our next question is: Which premise or premises support that conclusion most directly? What goes on the next level up on our diagram?
It seems fairly clear that proposition 13 belongs on that level. The question is whether it is alone there, with an arrow from 13 to 1, or whether it needs some help. The answer is that it needs help. This is the general/particular pattern we identified above. The conclusion is about a particular individual—Watson. Proposition 13 is entirely general (presumably Holmes knows this because he reads the paper and knows the disposition of Her Majesty’s troops throughout the Empire); it does not mention Watson. So proposition 13 needs help from other propositions that give us the relevant particulars about the individual, Watson. A number of conditions are laid out that a person must meet in order for us to conclude that they’ve been in Afghanistan: army doctor, being in the tropics, undergoing hardship, getting wounded. That Watson satisfies these conditions is asserted by, respectively, propositions 4, 5, 9, and 11. Those are the propositions that must work jointly with the general proposition 13 to give us our particular conclusion about Watson:

Next, we must figure out how what happens at the next level up. How are propositions 4, 5, 13, 9, and 11 justified? As we noted, the justification for 13 happens off-screen, as it were. Holmes is able to make that generalization because he follows the news and knows, presumably, that the only place in the British Empire where army troops are actively fighting in tropics is Afghanistan. The justification for the other propositions, however, is right there in the text.
Let’s take them one at a time. First, proposition 4: Watson is an army doctor. How does Holmes support this claim? With propositions 2 and 3, which tell us that Watson is a medical and a military man, respectively. This is another pattern we’ve identified: these two propositions jointly support 4, because they each provide half of what we need to get there. There are two parts to the claim in 4: army and doctor. 2 gives us the doctor part; 3 gives us the army part. 2 and 3 jointly support 4.
Skipping 5 (it’s a bit more involved), let’s turn to 9 and 11, which are easily dispatched. What’s the reason for believing 9, that Watson has suffered hardship? Go back to the passage. It’s his haggard face that testifies to his suffering. Proposition 10 supports 9. Now 11: what evidence do we have that Watson’s arm has been injured? Proposition 12: he holds it stiffly and unnaturally. 12 supports 11.
Finally, proposition 5: Watson was in the tropics. There are three propositions involved in supporting this one: 6, 7, and 8. Proposition 6 tells us Watson’s face is dark; 7 tells us that his skin isn’t naturally dark; 8 tells us his wrists are fair (light-colored skin). It’s tempting to think that 6 on its own—dark skin—supports the claim that he was in the tropics. But it does not. One can have dark skin and not visited the tropics, provided one’s skin is naturally dark. What tells us Watson has been in the tropics is that he has a tan—that his skin is dark and that’s not its natural tone. 6 and 7 jointly support 5. And how do we know Watson’s skin isn’t naturally dark? By checking his wrists, which are fair: proposition 8 supports 7.
So this is our final diagram:
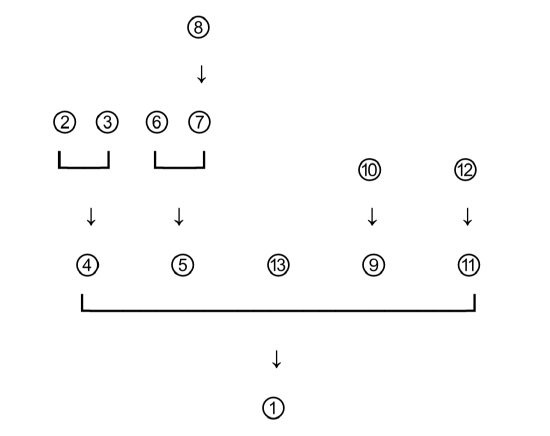
And there we go. An apparently unwieldy passage—thirteen propositions!—turns out not to be so bad. The lesson is that we must go step by step: start by identifying the conclusion, then ask which proposition(s) most directly support it; from there, work back until all the propositions have been diagrammed. Every long argument is just composed out of smaller, easily analyzed inferences.
Exercises
Diagram the following arguments.
1. ① Hillary Clinton would make a better president than Donald Trump. ② Clinton is a tough-minded pragmatist who gets things done. ③ Trump is a thin-skinned maniac who will be totally ineffective in dealing with Congress.
2. ① Donald Trump is a jerk who’s always offending people. Furthermore, ② he has no experience whatsoever in government. ③ Nobody should vote for him to be president.
3. ① Human beings evolved to eat meat, so ② eating meat is not immoral. ③ It’s never immoral for a creature to act according to its evolutionary instincts.
4. ① We need new campaign finance laws in this country. ② The influence of Wall Street money on elections is causing a breakdown in our democracy with bad consequences for social justice. ③ Politicians who have taken those donations are effectively bought and paid for, consistently favoring policies that benefit the rich at the expense of the vast majority of citizens.
5. ① Voters shouldn’t trust any politician who took money from Wall Street bankers. ② Hillary Clinton accepted hundreds of thousands of dollars in speaking fee from Goldman Sachs, a big Wall Street firm. ③ You shouldn’t trust her.
6. ① There are only three possible explanations for the presence of the gun at the crime scene: either the defendant just happened to hide from the police right next to where the gun was found, or the police planted the gun there after the fact, or it was really the defendant’s gun like the prosecution says. ② The first option is too crazy a coincidence to be at all believable, and ③ we’ve been given no evidence at all that the officers on the scene had any means or motivation to plant the weapon. Therefore, ④ it has to be the defendant’s gun.
7. ① Golden State has to be considered the clear favorite to win the NBA Championship. ② No team has ever lost in the Finals after taking a 3-games-to-1 lead, and ③ Golden State now leads Cleveland 3-to-1. In addition, ④ Golden State has the MVP of the league, Stephen Curry.
8. ① We should increase funding to public colleges and universities. First of all, ② as funding has decreased, students have had to shoulder a larger share of the financial burden of attending college, amassing huge amounts of debt. ③ A recent report shows that the average college student graduates with almost $30,000 in debt. Second, ④ funding public universities is a good investment. ⑤ Every economist agrees that spending on public colleges is a good investment for states, where the economic benefits far outweigh the amount spent.
9. ① LED lightbulbs last for a really long time and ② they cost very little to keep lit. ③ They are, therefore, a great way to save money. ④ Old-fashioned incandescent bulbs, on the other hand, are wasteful. ⑤ You should buy LEDs instead of incandescent bulbs.
10. ① There’s a hole in my left shoe, which means ② my feet will get wet when I wear them in the rain, and so ③ I’ll probably catch a cold or something if I don’t get a new pair of shoes. Furthermore, ④ having new shoes would make me look cool. ⑤ I should buy new shoes.
11. Look, it’s just simple economics: ① if people stop buying a product, then companies will stop producing it. And ② people just aren’t buying tablets as much anymore. ③ The CEO of Best Buy recently said that sales of tablets are “crashing” at his stores. ④ Samsung’s sales of tablets were down 14% this year alone. ⑤ Apple’s not going to continue to make your beloved iPad for much longer.
12. ① We should increase infrastructure spending as soon as possible. Why? First, ② the longer we delay needed repairs to things like roads and bridges, the more they will cost in the future. Second, ③ it would cause a drop in unemployment, as workers would be hired to do the work. Third, ④ with interest rates at all-time lows, financing the spending would cost relatively little. A fourth reason? ⑤ Economic growth. ⑥ Most economists agree that government spending in the current climate would boost GDP.
13. ① Smoking causes cancer and ② cigarettes are really expensive. ③ You should quit smoking. ④ If you don’t, you’ll never get a girlfriend. ⑤ Smoking makes you less attractive to girls: ⑥ it stains your teeth and ⑦ it gives you bad breath.
14. ① The best cookbooks are comprehensive, well-written, and most importantly, have recipes that work. This is why ② Mark Bittman’s classic How to Cook Everything is among the best cookbooks ever written. As its title indicates, ③ Bittman’s book is comprehensive. Of course it doesn’t literally teach you how to cook everything, but ④ it features recipes for cuisines from around the world—from French, Italian, and Spanish food to dishes from the Far and Middle East, as well as classic American comfort foods. In addition, ⑤ he covers almost every ingredient imaginable, with all different kinds of meats—including game—and every fruit and vegetable under the sun. ⑥ The book is also extremely well-written. ⑦ Bittman’s prose is clear, concise, and even witty. Finally, ⑧ Bittman’s recipes simply work. ⑨ In my many years of consulting How to Cook Everything, I’ve never had one lead me astray.
15. ① Logic teachers should make more money than CEOs. ② Logic is more important than business. ③ Without logic, we wouldn’t be able to tell when people were trying to fool us: ④ we wouldn’t know a good argument from a bad one. ⑤ But nobody would miss business if it went away. ⑥ What do businesses do except take our money? ⑦ And all those damned commercials they make; everybody hates commercials. ⑧ In a well-organized society, members of more important professions would be paid more, because ⑨ paying people is a great way to encourage them to do useful things. ⑩ People love money.


