3.1: The Basics

So far, we’ve discussed the basic ideas behind arguments or inferences. Each argument has premises which are the assumptions or the support of the argument. Each argument also has usually one, but sometimes more conclusions. The conclusion is the main point of the argument. The goal of any argument is to offer reasons for believing the conclusion. The reasons are the premises and the claim that you are supposed to accept if you agree with the argument is the conclusion.

So far so good. But there’s a lot more that we can say about arguments.

Ideally, when we’re trying to understand an argument fully—long before we decide whether or not we agree with the argument or whether or not it’s a good argument—we have a full grasp of the structure of the argument. That is, we need to know which premises go with which other premises, whether each premise is supposed to directly demonstrate the conclusion or is merely indirect support for the conclusion, etc. In short, we need a map or a diagram of the argument before we can decide whether or not it’s a good argument.

Simple arguments are called syllogisms: 2 premises and 1 conclusion and immediate inferences: 1 premise and 1 conclusion.

Like:

I like all vegetables

Carrots are a vegetable

So I like Carrots

Or:

I like all vegetables

So, there aren’t any vegetables I don’t like.

But normal arguments (arguments you’d find in a letter to the editor or in a social media post or on the radio or tv) aren’t like that—they have more premises, some of which don’t directly support the conclusion, but instead support other premises. It’s like a big complex argument that’s actually made out of smaller arguments.

So, if you want to understand how a complex argument in the real world hangs together, you need to be able to construct a map or diagram of that argument.

We’ll need to find out two things about each premise:

1. What kind of support does it offer for its conclusion? Does it support its conclusion in conjunction with other premises? Or does it instead form an argument by itself for the conclusion?

2. Does it support the main conclusion directly? Or does it instead support the conclusion indirectly by offering support for another premise, which in turn supports the main conclusion?

How do we go about actually building an Argument Map? Well, we could choose any convention at all, so we have to decide on what sorts of shapes, labels, symbols, etc. we’ll use for the sake of this course.

The first thing to note is that some people teach argument mapping going in an upwards direction—meaning that the conclusion would be on top and the premises for the conclusion would be below it. But we’re going to go a different way so that our argument maps more clearly track the usual format of an argument: the premises on top and the conclusion on bottom.

Here are some basic concepts and the associated conventional symbols and shapes:

We use arrows to signify Inferential Links or support. Every arrow means “implies that” or “therefore”. Read backwards (upwards), this diagram to the right means: “1 is true” “why?” “because of 2”. Or “Given that 2 is true, 1 follows.”	Paradigm Example: (1) We can go now, because (2) the car is packed.
Paradigm Example: (1) I know that Voodoo is real, because (2) My cousin saw someone take on the characteristics, personality, and voice of a spirit during a ceremony. (3) My cousin told me that she saw this last week.		Sometimes, we might find that a premise offers indirect support for the main conclusion of the argument. In that case, we have to build a vertical pattern into our argument map that might look something like the diagram to the left.

Conjoint vs. Independent Support

We need to be able to decide (once we’ve sorted out which are premises for which conclusion) what kind of support a set of premises provide for their conclusion. It’s independent support when each premise seems like it’s an argument for the conclusion on its own. It’s conjoint support when a premise doesn’t seem to support the conclusion without the help of the other premises. A good test for conjoint support is to pretend one of the premises is false. Does this affect the inference(s) from the other premise(s) to the conclusion?

Labradors are gentle, but they aren’t very aggressive,

so they wouldn’t make good guard dogs.

This feels like independent support because each inference makes sense on its own:

Labradors are gentle,

so they wouldn’t make good guard dogs.

Labradors aren’t very aggressive,

so they wouldn’t make good guard dogs.

Let’s look at another:

[1] Vegetables are healthy and [2] tomatoes are vegetables, so [3] tomatoes are healthy.

Since 1 is a general principle and 2 is an instance of that general principle (or something like that), it makes sense to think that they’re conjoint. Any time you see this pattern—where one premise is a definition or general claim and another premise is a more particular claim that falls under that definition or general claim—you’ll think that those premises are likely conjoint.

The "General-Specific Pattern

When you see two premises where one premise is a general definition, a generalization, a hypothetical or conditional, or a general principle, and the other premise is a specific claim about an individual under that generalization, those are almost certain to be conjoint premises.

Examples

• A motorbike is any two-wheeled motor-driven vehicle and that moped has two wheels that are driven by a motor, so...
• If anyone goes to the amusement park, they’re going to be exhausted at the end of the day; and Cheri went to Six Flags today, so...
• Lying is wrong, but getting out of trouble would require me to lie, so....

If we try negating 2, then the inference doesn’t make any sense:

[1] Vegetables are healthy and [2] tomatoes are not vegetables, so [3] tomatoes are healthy.

What????

If we try negating 1, the inference falls apart again:

[1] Vegetables are unhealthy and [2] tomatoes are vegetables, so [3] tomatoes are healthy.

What??????

Let’s try one more slightly more complex conjoint support example:

Example \(\PageIndex{1}\)

[1] Gina told me the Earth is round and [2] Gina wouldn’t lie to me, and furthermore [3] Gina is an astrophysicist, so [4] the Earth is round.

Let’s try the negation test on 1:

[1] Gina told me the Earth is flat and [2] Gina wouldn’t lie to me, and furthermore [3] Gina is an astrophysicist, so [4] the Earth is round.

What??? Let’s try it on 2:

[1] Gina told me the Earth is round and [2] Gina often lies to me, and furthermore [3] Gina is an astrophysicist, so [4] the Earth is round.

What???? Let’s try it on 3:

[1] Gina told me the Earth is round and [2] Gina wouldn’t lie to me, and furthermore [3] Gina is not an astrophysicist, so [4] the Earth is round.

Well... this isn’t as incoherent as the other examples. But why mention that Gina is an astrophysicist at all if it doesn’t at least help 1 and 2 demonstrate the conclusion that the Earth is round? With the negation of 3 as part of the argument, it seems thoroughly awkward that we should be talking about Gina being or not being an astrophysicist at all. If anything, it seems to work against the inference.

What’s the lesson here? The negation test isn’t perfect, but it does almost always reveal when you’ve got a premise that seems to work together with other premises. In the Gina case, we’ve got a premise that is closely related in subject matter and so we’ve got some reason to conjoin it with 1 and 2.

Here’s how we go about mapping conjoint vs. independent support once we’ve decided what sort of support is involved.

Mapping Independent Support

Example \(\PageIndex{2}\)

We use multiple arrows to signify multiple independent inferences. So, we have many premises which do not work together to demonstrate the conclusion. Each premise offers its own reason for accepting the conclusion.

Paradigm example:

(1) This test is easy.

(2) Tetsuo got an A on the test and

(3) Xochitl got an A on the test and

(4) Francisco got an A on the test.

If the other premises were not there, the argument would not fall apart. The premises don’t need each other to be true to support the conclusion.

“Given 2, 1 follows, and given 3, 1 follows, and given 4, 1 follow.”

Independent support is really like having multiple inferences. So the map above seems to tell us that there are three separate inferences that just happen to have the same conclusion.

Mapping Conjoint Support

Example \(\PageIndex{3}\)

We use brackets to signify a single inference with many conjoint or mutually dependent premises. The premises work together to support the conclusion. Without the other conjoint premises, it would be unclear why one conjoint premise should be taken as a reason for accepting the conclusion.

Paradigm example:

(1) You are behaving unfairly.

(2) You’re giving more to some than to others and

(3) giving more to some than to others isn’t fair.

If any one of them is false or wasn’t there to begin with, the inference falls apart.

“Given 2, 1 doesn’t follow unless we also have 3 (and 4, 5, 6, ...).”

Deductive arguments are more often than not conjoint support. This is just a rough and ready rule, but the way standard Deductive arguments (without extra irrelevant premises) work is that the premises are all necessary for the inference to demonstrate the conclusion. So it makes sense that they would be conjoint premises.

Here’s a complete example of a problem like you might see on a quiz or exam (though they’ll usually be less complex than these, at least to start out).

Example \(\PageIndex{4}\)

(1) Government mandates for zero-emission vehicles won’t work because (2) only electric cars qualify as zero-emission vehicles, and (3) electric cars won’t sell. (4) They are too expensive, (5) their range of operation is too limited, and (6) recharging facilities are not generally available.

Adding in 3 makes the inference make sense again (Oh, I see, electric cars won’t solve our problems). You can do the same by taking 2 away. Wait, we’ll say, what about other zero-emission vehicles??? Adding 2 back in makes sense of the inference.

4, 5, and 6 are independent because they don’t have much to do with one another. The inference from 4 to 3, 5 to 3, and 6 to 3 all makes sense. “They’re too expensive, so they won’t sell.” (makes sense). “Their range is limited, so they won’t sell” (makes sense). “There aren’t enough recharging facilities, so they won’t sell” (makes sense!).

Example \(\PageIndex{5}\)

We also use downward braces if there are more than one conclusion for any given inference. This is called Multiple Conclusions.

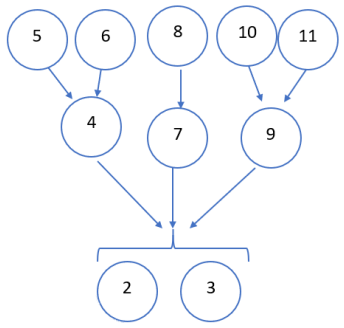
Example:

(1) The president may have her faults, but

(2) she is an outstanding leader and

(3) we should reelect her.

(4) Her foreign policy has brought about respite from violence in various war torn regions as

(5) she sent in troops to protect refugees in Rwanda and (6) she negotiated an armistice between Egypt and Israel. (7) Her economic policy has also been largely successful in that (8) a potential recession has been avoided for now. (9) She is also a great moral leader as (10) hers is a model family and (11) she demonstrates true integrity daily.

Notice how 1 isn’t actually part of the argument: it just introduces the topic but isn’t a premise or conclusion. 2 and 3 are both conclusions (notice the “and”, which often links premises to premises and conclusions to conclusion) because neither is a premise/evidence for the other and both are implied by the rest of the argument (4, 7, and 9).

Why did we go with independent support for all of the top-most premises? Try to reason through it on your own.

Terminology

Let’s introduce some new terminology so we can have a common language with which to talk about arguments:

• A “level” or “layer” of an argument map is one horizontal row of a carefully-drawn argument map. Notice how the previous argument map above is drawn so that even though there’s a lot going on in the argument, we can see 3 distinct layers or horizontal rows?
• A Main Conclusion is the final conclusion of the argument. It doesn’t serve as a premise/support for any other proposition in the complex argument. It’s always in the bottom-most layer
• A Main Premise is one among the set of premises that directly support the main conclusion. It’s always in the layer that’s the second from the bottom.
• A Sub-Inference is an inference from a premise to another premise. The conclusion of a sub-inference is never in the bottom-most layer.
  • A sub-premise is a premise in a sub-inference.
  • A sub-conclusion is a conclusion in a sub-inference. (Note that a sub-conclusion is always a premise itself, and that it is usually one of the main premises unless the argument gets really complex).

So here it is, the anatomy of a typical 3-layer argument diagram:

The following excerpt from Knachel’s text covers some of the same ground we just covered, but sometimes it’s helpful to see a different explanation of the same thing:

From: Knachel, Matthew, "Fundamental Methods of Logic" (2017).

Philosophy Faculty Books. 1. http://dc.uwm.edu/phil_facbooks/1

Creative Commons Attribution 4.0 International License

V. Diagramming Arguments

Before we get down to the business of evaluating arguments—of judging them valid or invalid, strong or weak—we still need to do some preliminary work. We need to develop our analytical skills to gain a deeper understanding of how arguments are constructed, how they hang together. So far, we’ve said that the premises are there to support the conclusion. But we’ve done very little in the way of analyzing the structure of arguments: we’ve just separated the premises from the conclusion. We know that the premises are supposed to support the conclusion. What we haven’t explored is the question of just how the premises in a given argument do that job—how they work together to support the conclusion, what kinds of relationships they have with one another. This is a deeper level of analysis than merely distinguishing the premises from the conclusion; it will require a mode of presentation more elaborate than a list of propositions with the bottom one separated from the others by a horizontal line. To display our understanding of the relationships among premises supporting the conclusion, we are going to depict them: we are going to draw diagrams of arguments.

Here’s how the diagrams will work. They will consist of three elements: (1) circles with numbers inside them—each of the propositions in the argument we’re diagramming will be assigned a number, so these circled numbers in the diagram will represent the propositions; (2) arrows pointed at circled numbers—these will represent relationships of support, where one or more propositions provide a reason for believing the one pointed to; and (3) horizontal brackets—propositions connected by these will be interdependent (in a sense to be specified below).

Our diagrams will always feature the circled number corresponding to the conclusion at the bottom. The premises will be above, with brackets and arrows indicating how they collectively support the conclusion and how they’re related to one another. There are a number of different relationships that premises can have to one another. We will learn how to draw diagrams of arguments by considering them in turn.

Independent Premises

Often, different premises will support a conclusion—or another premise—individually, without help from any others. When this is the case, we draw an arrow from the circled number representing that premise to the circled number representing the proposition it supports.

Consider this simple argument:

\(\require{enclose} \enclose{circle}{\kern .06em 1\kern .06em}\) Marijuana is less addictive than alcohol. In addition, \(\enclose{circle}{\kern .06em 2\kern .06em}\) it can be used as a medicine to treat a variety of conditions. Therefore, \(\enclose{circle}{\kern .06em 3\kern .06em}\) marijuana should be legal.

The last proposition is clearly the conclusion (the word ‘therefore’ is a big clue), and the first two propositions are the premises supporting it. They support the conclusion independently. The mark of independence is this: each of the premises would still provide support for the conclusion even if the other weren’t true; each, on its own, gives you a reason for believing the conclusion. In this case, then, we diagram the argument as follows:

Intermediate Premises

Some premises support their conclusions more directly than others. Premises provide more indirect support for a conclusion by providing a reason to believe another premise that supports the conclusion more directly. That is, some premises are intermediate between the conclusion and other premises.

Consider this simple argument:

\(\enclose{circle}{\kern .06em 1\kern .06em}\) Automatic weapons should be illegal. \(\enclose{circle}{\kern .06em 2\kern .06em}\) They can be used to kill large numbers of people in a short amount of time. This is because \(\enclose{circle}{\kern .06em 3\kern .06em}\) all you have to do is hold down the trigger and bullets come flying out in rapid succession.

The conclusion of this argument is the first proposition, so the premises are propositions 2 and 3. Notice, though, that there’s a relationship between those two claims. The third sentence starts with the phrase ‘This is because’, indicating that it provides a reason for another claim. The other claim is proposition 2; ‘This’ refers to the claim that automatic weapons can kill large numbers of people quickly. Why should I believe that they can do that? Because all one has to do is hold down the trigger to release lots of bullets really fast. Proposition 2 provides immediate support for the conclusion (automatic weapons can kill lots of people really quickly, so we should make them illegal); proposition 3 supports the conclusion more indirectly, by giving support to proposition 2. Here is how we diagram in this case:

Joint Premises

Sometimes premises need each other: the job of supporting another proposition can’t be done by each on its own; they can only provide support together, jointly. Far from being independent, such premises are interdependent. In this situation, on our diagrams, we join together the interdependent premises with a bracket underneath their circled numbers.

There are a number of different ways in which premises can provide joint support. Sometimes, premises just fit together like a hand in a glove; or, switching metaphors, one premise is like the key that fits into the other to unlock the proposition they jointly support. An example can make this clear:

\(\enclose{circle}{\kern .06em 1\kern .06em}\) The chef has decided that either salmon or chicken will be tonight’s special. \(\enclose{circle}{\kern .06em 2\kern .06em}\) Salmon won’t be the special. Therefore, \(\enclose{circle}{\kern .06em 3\kern .06em}\) the special will be chicken.

Neither premise 1 nor premise 2 can support the conclusion on its own. A useful rule of thumb for checking whether one proposition can support another is this: read the first proposition, then say the word ‘therefore’, then read the second proposition; if it doesn’t make any sense, then you can’t draw an arrow from the one to the other. Let’s try it here: “The chef has decided that either salmon or chicken will be tonight’s special; therefore, the special will be chicken.” That doesn’t make any sense. What happened to salmon? Proposition 1 can’t support the conclusion on its own. Neither can the second: “Salmon won’t be the special; therefore, the special will be chicken.” Again, that makes no sense. Why chicken? What about steak, or lobster? The second proposition can’t support the conclusion on its own, either; it needs help from the first proposition, which tells us that if it’s not salmon, it’s chicken. Propositions 1 and 2 need each other; they support the conclusion jointly. This is how we diagram the argument:

The same diagram would depict the following argument:

\(\enclose{circle}{\kern .06em 1\kern .06em}\) John Le Carre gives us realistic, three-dimensional characters and complex, interesting plots. \(\enclose{circle}{\kern .06em 2\kern .06em}\) Ian Fleming, on the other hand, presents an unrealistically glamorous picture of international espionage, and his plotting isn’t what you’d call immersive. \(\enclose{circle}{\kern .06em 3\kern .06em}\) Le Carre is a better author of spy novels than Fleming.

In this example, the premises work jointly in a different way than in the previous example. Rather than fitting together hand-in-glove, these premises each give us half of what we need to arrive at the conclusion. The conclusion is a comparison between two authors. Each of the premises makes claims about one of the two authors. Neither one, on its own, can support the comparison, because the comparison is a claim about both of them. The premises can only support the conclusion together. We would diagram this argument the same way as the last one.

Another common pattern for joint premises is when general propositions need help to provide support for particular propositions. Consider the following argument:

We shouldn’t elect someone who has proven an incompetent business leader.

Candidate Z has proven an incompetent CEO. So, we shouldn’t elect Candidate Z.

These premises will be mapped with conjoint support since the premises need to work together to show the conclusion. One general principle about who we shouldn’t elect, and one particular claim about Candidate Z.

End Knachel Text

Examples

Let’s walk through a few examples of arguments that need mapping:

Example \(\PageIndex{6}\)

She's the best girlfriend ever. She bought me a new backpack for Christmas, she's never late for a date, and she always treats me with care.

Solution

First, we need to identify each proposition—that is, each claim that can be true or false independently of the other claims. This is a bit interpretive, so sometimes there aren’t hard and fast rules that produce one particular right answer, but generally we can all come up with the same propositions:

(1) She's the best girlfriend ever. (2) She bought me a new backpack for Christmas, (3) she's never late for a date, and (4) she always treats me with care.

What a nice young person! Next, we need to decide what the conclusion is and which propositions are premises. A nice test that often helps is to read all of the premises and then say “therefore...” and then read what you think is the conclusion. It should make sense as an inference if you do this properly. For instance, this is clearly not so good:

She’s the best girlfriend ever, she bought me a new backpack, and she always treats me with care, therefore she’s never late for a date.

Uhhhhh...what?

This one sounds a lot more sensical:

She bought me a new backpack, she’s never late for a date, and she always treats me with care, therefore she’s the best girlfriend ever.

It seems like the three premises are evidence for the claim that she is the best girlfriend ever. The thing we’re being asked to believe as a result of this reasoning is that she’s the best girlfriend ever. So that is the conclusion of the inference.

Now we’ve already basically ruled out that 2, 3, and 4 have any inferential relationship between them. They all seem to give us reasons for believing the conclusion directly. Furthermore, none of them seems to give us reason for believing any other. Maybe 4 could be the conclusion of 2, but that’s a real stretch. So based on all of this, we can reasonably conclude that 2, 3, and 4 are all on the same level and are all main premises for the conclusion.

Next, we need to decide if these are conjoint or independent premises. What do you think?

How do we decide? Using the negation test. If negating or saying the opposite of one premise doesn’t make the inference fall apart, then the premises are not conjoint—they’re independent. Let’s try it here:

She bought me a new backpack, she’s sometimes late for a date, and she always treats me with care, therefore she’s the best girlfriend ever.

I mean, it is a bit weird, but it’s not nonsense. Sure, she’s sometimes late for a date, but the inference still makes sense.

She hasn’t bought me a new backpack, but she’s never late for a date, and she always treats me with care, therefore she’s the best girlfriend ever.

Again, it’s strange, but not nonsensical. We wonder why the backpack thing is brought up in the first place, but we don’t immediately think “oh, well, she can’t be the best girlfriend ever if she hasn’t bought you a backpack!” Instead, we just think, “she’s clearly an excellent partner, backpack or none.”

The last one is a bit stranger:

She bought me a new backpack, she’s never late for a date, but she doesn’t always treat me with care, therefore she’s the best girlfriend ever.

Interesting...the case is definitely pretty weak for her being the bester girlfriend ever at this point, but the inference hasn’t utterly fallen apart. An opposite conclusion doesn’t now follow, we just have weaker reason for accepting the conclusion than we had before. This test reveals how strong a piece of evidence proposition 4 was for the conclusion in the original argument, but it doesn’t tell us that 4 is conjoint—the argument didn’t fall apart.

With all of this in mind, the premises appear to be independent reasons from one another for accepting the conclusion that she is the best girlfriend ever. So the argument map looks like so:

How about another example? This time I’ve skipped right to numbered propositions:

Example \(\PageIndex{7}\)

(1) Obama was the best President in American history. (2) He protected people with pre-existing medical conditions from certain financial ruin or death by passing the Affordable Care Act, and (3) that feat was among the greatest legislative victories an American President has ever known. (4) He was able to topple the head of Al-Qaida and the mastermind of the 9/11 attacks, and (5) he oversaw the recovery from the largest economic disaster since the Great Depression. (6) Anyone who could bring us back from the brink of global economic meltdown to a stable and healthy economic like we had at the end of his tenure must be a truly great president.

Solution

Before we ever get to the question of whether or not this is a good argument, or what’s wrong with it if anything, or whether or not the conclusion is true, we must understand the argument. In particular we must understand the structure of the argument. This argument is complex, so what’s going on here?

What’s the conclusion? It’s probably somewhat obvious here. There’s one claim that seems like the kind of claim someone might have as a thesis statement, or might defend in an Oxford-style debate. There’s one claim that seems to unify the rest of the propositions: everything is meant to justify or defend the claim that Obama was the best President in American history.

With a longer argument like this, sometimes it is best to simply work sentence-by-sentence. 2 and 3 are part of the same sentence. The “and” tells us that there probably is no inferential link between 2 and 3. “and” is usually not interchangeable with “therefore”. When we read the content of 2 and 3, furthermore, 3 makes reference to 2. Often when a premise makes reference to another premise we can conclude that they are conjoint premises. Not always, mind you, and often that means that one is a subpremise for the other. Nevertheless, in this case the reference to “that feat” in 3 ties 3 to 2 conjointly. We can run the negative test to be sure we’re correct here:

(1) Obama was the best President in American history. (2) He protected people with pre-existing medical conditions from certain financial ruin or death by passing the Affordable Care Act, and (3) that feat was an unremarkable legislative accomplishment.

Now I’m unclear why we should think he’s the best president in history if the reason we’re being given is that he passed an important, but unremarkable piece of legislation. Not convincing. If anything, it seems to suggest that he was a fine, but unremarkable president.

(1) Obama was the best President in American history. (2) He didn’t protect people with pre-existing medical conditions from certain financial ruin or death by passing the Affordable Care Act, and (3) that feat would have been among the greatest legislative victories an American President has ever known.

Ummm...no. His not passing landmark legislation doesn’t make him the best president.

This is one way you know you’re dealing with conjoint premises: if one premise explains how the other premise supports the conclusion.

So these two premises are conjoint. What about 4? It’s part of the same sentence as 5, but the topics are so wildly different that it’s hard to see how they could be conjoint premises. Instead, it seems safe to assume they’re independent and that they’re independent from 2 and 3 for the same reason. They do, however, appear to be premises for the main conclusion (1) and so appear to belong on the second level with the other main premises 2 and 3.

The last proposition, though, seems to essentially be about the same topic as 5 and furthermore seems to be the reason 5 supports the conclusion. This is one way you know you’re dealing with conjoint premises: if one premise explains how the other premise supports the conclusion. So 6 and 5 appear to be conjoint. If you ran the negative test, you’d soon learn that the negated inferences make no sense.

As a result, the whole argument map, which is a bit strange looking, looks like this: