1.1: Introduction
- Page ID
- 52061
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Imagine that you are not reading this textbook. Imagine instead that you are lying on your back in some soft grass on a warm summer night, far from city lights, staring into the vast, dark night sky. As you continue to gaze at the stars, you would likely notice that over the course of hours they all slowly move – in unison – in the same direction. From the Northern Hemisphere, you will always see the constellation Canis Major near Orion, or the constellation of the Celestial Bear flanked by its seven hunters, but all of them will seem to rotate around Polaris, the North Star. If you are incredibly perceptive, however, you may notice that not all points of light in the night sky move together. Some of them follow their own path, wandering through the sky with the stars as a backdrop. The ancient Greeks called them asteres planetai, meaning wandering stars, which is where we get the word planet from. If you were to carefully track the path of a planet over the course of a few nights, you would realize that – even though its movement is different from that of the stars – it is far from random. It follows a certain path through the night sky. Indeed, while different planets follow different paths, you could begin to notice similarities between the motions of all the planets as they wander through the heavens. Observed from the Earth, they all appear to move in an eastward direction, and their paths are roughly on the same plane.
But why? What kind of explanation could we give for why planets’ paths differ from those of the stars? Why do planets seem to behave in very similar ways to one another? What are the best scientific theories we have to explain planetary motion?
Let’s try a familiar explanation. Those planets are actually no different from the Earth: they are large massive objects, all orbiting around a much more massive object in the centre of our solar system – the Sun. Isaac Newton showed in his law of universal gravitation that the very same force which pulls an apple to the ground, and which causes the parabolic paths of projectiles, also causes planets and moons to take the precise paths they do through space. The speed of the planets and the force of gravity keep planets like the Earth and Mars in orbit around the Sun. From the vantage point of Earth, therefore, planets seem to wander through the night sky because they are following their own, elliptical paths around our nearby Sun. Meanwhile, the constellations and positions of the stars remain relatively fixed because they are so far away from the solar system, and they rotate together due to the rotation of the Earth on its axis. This is the answer you would receive if you were able to travel back to the year 1800 and ask a member of the scientific community at the Royal Society in London, England to give you their best, agreed-upon scientific theories about planetary motion.
But what if we were to travel even further back in time, say 500 years? What accepted theories would an astronomer from the University of Paris in the year 1500 use to explain the wandering of the planets? A late-medieval astronomer would explain planetary motion by referencing Aristotelian natural philosophy. This set of theories accounted for the motion of objects by considering the movements that are natural to different elements. It was believed at the time that the universe is made of two completely distinct regions – terrestrial and celestial. Everything in the terrestrial region was thought to be composed of a certain combination of the four terrestrial elements – earth, water, air, and fire. The elements earth and water were believed to be heavy, while the elements air and fire were believed to be light.

Each of the four elements was thought to have a natural position to which it is predisposed. For heavy elements, the natural position is the centre of the universe, which explained why everything made of elements earth and water has a tendency to fall down. This is why, they would say, when you drop a rock it goes straight down. This would also suggest that the terrestrial globe, which is predominantly a combination of the elements earth and water, should necessarily be at the centre of the universe. In the celestial region, in contrast, everything, including the planets and the stars, was believed to be made of a completely different element, aether. The natural tendency of aether is to revolve in a circular path around the centre of the universe. The planets, being between the stationary sphere of the Earth and the slowly-rotating stars, naturally follow their own circular paths through the night sky, accounting for their apparent “wandering” in front of the distant stars.
Tired of all this hypothetical time travel, let’s say you made an actual voyage to the Mauna Kea Observatories in Hawaii, USA, and – after a relaxing day at the beach – asked a modern-day astronomer to explain planetary motion using the best, agreed-upon scientific theories. The astronomer would not give you the Aristotelian-Medieval answer, nor would they give you the Newtonian answer you may be familiar with from basic physics or astronomy classes. The accepted view today is that the paths of the planets, like the Earth, are best explained by Albert Einstein’s theory of general relativity, not Newton’s law of universal gravitation. Today, the elliptical paths of planets around the sun are not taken to be due to a force called gravity but are rather due to the fact that the mass of our Sun bends the fabric of space-time itself. Imagine a region of space-time without any material objects. Such a region would be completely flat. What this means is that in such a space, light rays would travel along straight lines, and the geometry we learned in secondary school, Euclidean geometry, will hold exactly.

Now, let’s add a star to this region of space. According to general relativity, this star will curve the space-time around it, affecting the motion of all other material processes in its vicinity, including light rays. The space will no longer be exactly describable by Euclid’s geometry, but rather by a geometry developed by the German mathematician Herman Minkowski and incorporated by Einstein into his theory. This geometry treats time as a fourth dimension, perpendicular to the familiar three dimensions of length, width, and breadth, which is why we speak of space-time. Even physicists can’t really picture all this. They can represent the situation using mathematical equations and make predictions by solving them. They understand these mathematical models by using analogies that involve fewer dimensions. As an example of such an analogy, let’s imagine a stretched bedsheet with a basketball placed in the middle of it. The basketball will make a dip in the bedsheet. The two-dimensional bedsheet represents four-dimensional space-time. The dip in the bedsheet in the third dimension produced by the ball represents the curvature of four-dimensional space-time produced by an object with mass, like a star. Now, let’s roll a tennis ball across the bedsheet. Because the fabric of the bedsheet is curved by the basketball, the tennis ball will not move in a straight line, but rather will have a curved trajectory along the bedsheet. It will appear as though the tennis ball is attracted by the basketball, while in fact it is merely following the curvature of the bedsheet. According to general relativity, something like this happens when a region of space-time is curved by a massive object, such as a star, with the tennis ball being something like a planet moving on a curved trajectory through space near the star.
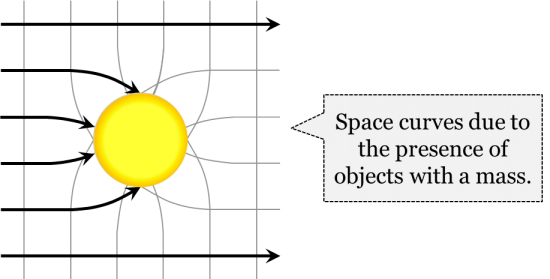
The same goes for any object with mass. The reason the Moon or a spacecraft continues to revolve around the Earth is that the Earth, as a massive object, bends the space-time around it to capture the Moon in a sort of dip in space-time. Similarly, the Sun, a significantly more massive object, bends a larger region of space-time than the Earth and captures the Earth, the planets, and many other celestial objects in its larger dip in space. The degree of curvature of space-time around an object depends on both the mass of an object and on how compressed that mass is into a small region of space. If any object is compressed within its Schwarzschild radius, named for the German physicist Karl Schwarzschild, the curvature of space will become so great that even light rays cannot escape it. It will become a black hole. The Schwarzschild radius of the Earth is 8.7 millimetres. If the Earth were somehow compressed to this tiny radius, it would become a black hole. Although in the 2009 Star Trek movie, malevolent aliens destroyed the planet Vulcan this way, astrophysicists don’t know of any natural process that would crush a planet to such densities. The only known natural process that can crush an object to within its Schwarzschild radius is the collapse of a massive star that has exhausted its nuclear fuel, and this is how astrophysicists suppose black holes form.

What this means is that the seeming attraction between two material objects is nothing but an inertial motion in a curved space. According to general relativity, there is no force of gravity; all material objects curve the space around them to a greater or lesser degree and this curvature affects the motion of other material objects which happen to be in the vicinity, just like the motion of the tennis ball on a suspended bedsheet. Note that physicists still use the word “gravity” as a shortcut for “motion in a curved space-time”. Yet, strictly speaking, in general relativity the seeming gravitational attraction among material objects is understood as merely a motion in a space-time which is not flat but curved by material objects. A planet’s elliptical orbit, therefore, is not because of gravity, but because of a combination of that planet’s own momentum and the shape of the space-time bent by the Sun’s mass.
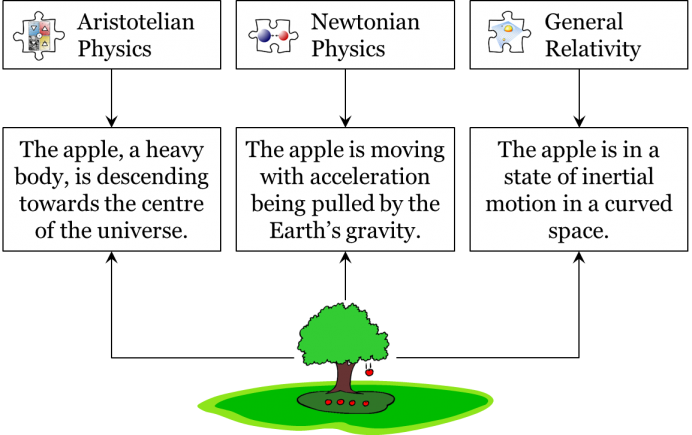
In short, the best astronomical theories from different historical periods explained the motion of the planets in very different ways. But the scientific communities in any one of these periods didn’t just agree on astronomy! In addition to astronomical and physical theories, the scientific communities of each of these periods also accepted a variety of theories on different natural, social, formal, and artificial objects. Considered together, these individual theories from any one historical moment can be shown to make up a complex, interwoven tapestry of theories, constituting that historical community’s best available description of the world. Take, for instance, the theories that we accept nowadays. If we were to ask a scientist what theories best describe the world, they would probably mention several theories from natural science, such as general relativity, quantum physics, big bang cosmology, contemporary chemistry, the modern evolutionary synthesis in biology, etc. They would also likely mention some theories from social science, such as those from psychology, economics, or sociology. In addition, they would probably mention a few theories that pertain to formal science, including mathematics and logic. Here is a snapshot of some of the theories accepted these days:

This interlocking jigsaw puzzle represents many of this community’s best available descriptions of the world – their accepted theories. Taken together, we call this complete set of a community’s accepted theories its mosaic.

Mosaics change through time as scientific communities accept new theories and reject old ones. Here is a quick snapshot of a typical mid-18th-century Newtonian mosaic:
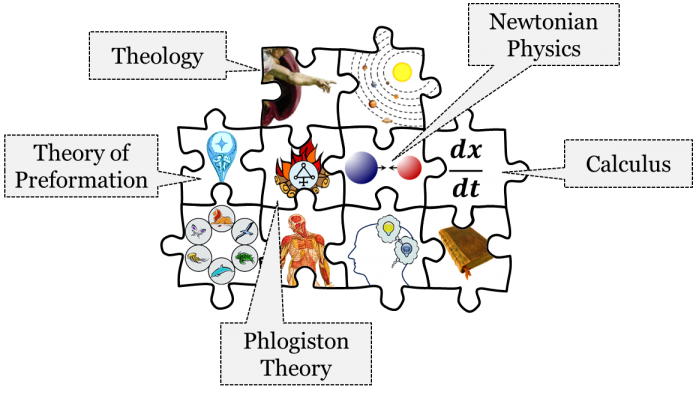
Among other things, this mosaic included Newtonian physics with its three laws of mechanics and the law of gravity, the chemical theory of phlogiston, and even theology, the study of God and his works.
Finally, here are some of the theories of the Aristotelian-Medieval mosaic:

Notice the presence of Aristotelian natural philosophy with its theory of four terrestrial and one celestial element, theology, and, interestingly, astrology, the study of celestial influences on terrestrial affairs.
Mosaics and changes in them are the central focus of this textbook. For any point in history, a community’s mosaic showcases its best attempt to understand reality, in all its dynamism and complexity. This drive to understand reality is a human one, which means that individuals – in their social and institutional contexts – are important parts of the story of how certain theories come to be, and how those theories come to change. For instance, to better understand the theories of planetary motion we sketched earlier, we could trace the histories of institutions like the Royal Society in England, the University of Paris, or the Mauna Kea Observatories in the U.S.A., or of individual investigators at any one of those institutions. One can certainly come to appreciate science’s history by approaching it this way! But a different kind of appreciation for science can be gained by taking a step back and seeing these astronomical theories as one facet of the total set of the best theories accepted by the scientific community of the time. Focusing on the mosaics of general scientific communities allows us to get the “big picture” of how scientific knowledge – writ large – has changed through time, without necessarily excluding or sacrificing that particular data of who was producing that knowledge, where, and under what specific circumstances.
Considering science from this broad historical perspective sheds light on some of the perennial questions in the philosophy of science. Philosophy of science asks questions that attempt to clarify exactly what science is, how it is different from other human endeavours, and how it works. We will take the opportunity to engage with the following pivotal questions of the philosophy of science in the first half of this textbook, all the while drawing from the rich history of science:
- Absolute Knowledge: Is there anything we can know with absolute certainty? That is, are there any theories in the mosaic that will never be replaced, that are established beyond any reasonable doubt? (Chapter 2)
- Scientific method: How do scientists evaluate competing theories? What are the criteria they employ to assess theories? (Chapter 3)
- Laws of Scientific Change: What is the mechanism of scientific change? How do mosaics and their elements change through time? Is there a pattern to those changes? (Chapter 4)
- Scientific Progress: Are our theories becoming better descriptions of reality? Is there such thing as scientific progress? (Chapter 5)
- Science and Non-science: What’s the difference between science and non-science? What differentiates scientific theories from unscientific theories and scientific changes from unscientific changes? (Chapter 6)
Our culture is saturated by scientific claims and the technological results of scientific investigations. We are used to hearing about scientific discoveries in popular news media. Careers increasingly require a level of scientific literacy, and you may even be pursuing a career as a practicing scientist. This is all to say that we talk about “science” all the time. But have we really taken the time to think about what science is, how scientific theories are accepted and rejected, and the degree of certainty we can have about scientific claims? Engaging with the aforementioned questions in the first chapters is an opportunity to do just that – to look at science from a new perspective, with fresh eyes.
After having done so, we will trace the genealogy of our contemporary scientific worldview by examining the mosaics of four key historical moments and addressing two key historical questions:
What was the content of the mosaic at each of these four moments?
How do these mosaics change over time?
That is, what theories did that community actually consider to be the best available in each scientific field/discipline (astronomy, physics, biology, etc.) in any given historical period and what led to the eventual replacement of those theories? In chapter 7, we will dive into the beautiful systematicity of the Aristotelian-Medieval worldview, shedding light on the theories which made up their cosmology, physics, and informed their medical practices. In chapter 8, we will turn to a lesser-known and underappreciated worldview in the history of science – the Cartesian worldview. We will turn to the Newtonian worldview in chapter 9, with a focus on how its mosaic eventually replaced the Cartesian worldview in Europe and represented the final shift away from the Aristotelian-Medieval worldview. Finally, in chapter 10, we will consider how the acceptance of a key set of new theories led to the shift from the Newtonian to the Contemporary scientific worldview, returning us to the present.
With a greater grasp of science’s history and philosophy under our belts, we will bring them both together in our concluding chapter 11. Here, we will discuss the metaphysics of science and how mosaics shape metaphysical assumptions and, concomitantly, worldviews. Additionally, chapter 11 will be an opportunity to consider the limitations of an introductory textbook to so vast a topic, but we will do so by directing you to fascinating avenues of further research.


