3.4: Operations on Categorical Sentences
- Page ID
- 24330
We continue our exploration of the portion of natural language to which Aristotle’s logic restricts itself—the standard form sentences expressing categorical propositions. To familiarize ourselves more intimately with these, we will look at how they respond when we perform various operations on them, when we manipulate them in various ways. We will examine three operations: conversion, obversion, and contraposition. Each of these alters the standard form sentences in some way. The question we will ask is whether the new sentence that results from the manipulation is equivalent to the original sentence; that is, does the new sentence express the same proposition as the original?
Conversion
Performing conversion on a categorical sentence involves changing the order of the subject and predicate terms. The result of this operation is a new sentence, which is said to be the converse of the original sentence. Our question is: when does performing conversion produce an equivalent new sentence, a converse that expresses the same proposition as the converted original? We will look at all four types standard form sentence, answering the question for each.
Let’s perform conversion on a sentence expressing a universal affirmative, A proposition and see what happens. ‘All dogs are animals’ is such a sentence. conversion switches the subject and predicate terms, so the converse sentence is ‘All animals are dogs’. Does the converse express the same proposition as the original? Are they equivalent? Heck, no! The original sentence expresses the true proposition that all dogs are animals; the converse expresses the utterly false proposition that all animals are dogs. Converting an A sentence produces a new sentence that is not equivalent to the original.
This means that the effect on truth-value, in the abstract, of converting A sentences, is unpredictable. Sometimes, as with ‘All dogs are animals’, conversion will lead you from a truth to a falsehood. Other times, it may lead from truth to truth: ‘All bachelors are unmarried men’ and ‘All unmarried men are bachelors’ express different propositions, but both of them are true (because it so happens that, by definition, a bachelor is just an unmarried man). conversion of an A could also lead from falsehood to falsehood, as with the transition from ‘All dogs are bats’ to ‘All bats are dogs’. And it could lead from falsehood to truth: just reverse the order of the first conversion we looked at, from ‘All animals are dogs’ to ‘All dogs are animals’.
Again, the point here is that, because conversion of A sentences produces a converse that expresses a different proposition than the original, we cannot know what the effect of the conversion will be on truth-value.
How about conversion of sentences expressing universal negative, E propositions? ‘No dogs are cats’ is such a sentence. Its converse would then be ‘No cats are dogs’. Are they equivalent? Yes, of course. Remember, an E proposition denies even partial inclusion; it makes the claim that the two classes involved don’t have any members in common. It doesn’t matter which of the two classes is listed first in the sentence expressing that proposition—you still get the assertion that the two classes are exclusive. This is true of E sentences generally: performing conversion on them always produces a new sentence that is equivalent to the original.
It is also true of sentences expressing particular affirmative, I propositions. ‘Some sailors are pirates’, after conversion, becomes ‘Some pirates are sailors’. These express the same proposition: they make the claim that the two classes have at least one member in common—there is at least one thing that is both a sailor and a pirate. Again, it doesn’t matter what order you put the class terms in; I sentences express the assertion that there’s overlap between the two classes. An I sentence and its converse are always equivalent.
The same cannot be said of sentences expressing particular negative, O propositions. Consider ‘Some men are not priests’. That expresses a true proposition. But its converse, ‘Some priests are not men’ expresses a different proposition; we know it’s a different proposition because it’s false. (As always, I’m using ‘priests’ to refer to Catholic priests, all of whom are men.) That is all we need to show that an operation does not produce equivalent sentences: one counterexample. As above with A sentences, this means that the effect on truth-value of converting O sentences is unpredictable. It can take us from truth to falsehood, as in this example, or from truth to truth, falsehood to falsehood, falsehood to truth. In the abstract, we cannot know the effect on truth of converting O sentences, since the converse expresses a different proposition from the original.
Summary for conversion: for E and I, converses are equivalent; for A and O, converses are not.
Obversion
Before we talk about our next operation, obversion, we need to introduce a new concept: class complements. The complement of a class, call it S, is another class which contains all the things that are not members of S. So, for example, the complement of the class of trees is just all the things that aren’t trees. The easiest way to name class complements is just to stick the prefix ‘non’ in front of the original class name. So the complement of trees is non-trees. Be careful: it may be tempting, for example, to say that the complement of Republicans is Democrats. But that’s not right. The complement of Republicans is a much bigger class, containing all the non-Republicans: not just Democrats, but Communists and Libertarians and Independents and Greens; oh, and a bunch of other things, too—like the planet Jupiter (not a Republican), my left pinkie toe, the Great Wall of China, etc., etc.
As a matter of notational convention, if we use a capital letter like S to refer to a class, we will denote the complement of that class as ~ S, which we’ll read as “tilde-S.”
Back to obversion. Here’s how this operation works: first, you change the quality of the sentence (from affirmative to negative, or vice versa); then, you replace the predicate with its complement. The result of performing obversion on a sentence is called the obverse of the original.
It turns out that performing obversion on a sentence always produces a new sentence that’s equivalent to it; a sentence and its obverse always express the same proposition. That means they share a truth-value: if a sentence is true, so is its obverse; if a sentence is false, its obverse is false, too. We can see that this is so by looking at the result of performing obversion on each of the four types of standard form sentences.
We’ll start with A sentences. Consider ‘All ducks are swimmers’. To perform obversion on this sentence, we first change its quality. This is a universal affirmative. Its quality is affirmative. So we change that to negative, keeping the quantity (universal) the same. Our new sentence is going to be a universal negative, E sentence—something of the form No S are P. Next, we replace the predicate with its complement. The predicate of the sentence is ‘swimmers’. What’s the complement of that class? All the things that aren’t swimmers: non-swimmers. So the obverse of the original A sentence is this: ‘No ducks are non-swimmers’.
Now, are these two sentences equivalent? Yes. ‘All ducks are swimmers’ expresses the universal affirmative proposition, asserting that the class of ducks is entirely contained in the class of swimmers. That is to say, any duck you find will also be in the swimmer class. Another way of putting it: you won’t find any ducks who aren’t in the class of swimmers. In other words, no ducks fail to be swimmers. Or: ‘No ducks are non-swimmers’. The A sentence and its obverse are equivalent; they express the same proposition, make the same claim about the relationship between the class of ducks and the class of swimmers.
Let’s try obversion on a universal negative, E sentence. ‘No women are priests’ is one. First, we change its quality from negative to affirmative: it becomes a universal affirmative, A sentence— something of the form All S are P. Next, we replace it predicate, ‘priests’, with its complement, ‘non-priests’. The result: ‘All women are non-priests’. Is that equivalent to the original? It tells us that all women are outside the class of priests. In other words, none of them are priests. That is, ‘No women are priests’. Yes, both the original sentence and its obverse tell us that the classes of women and priests are exclusive.
Next, the particular affirmative—an I sentence like ‘Some politicians are Democrats’. OK. First, change the quality—from affirmative to negative. Our obverse will be a particular negative, O sentence—something of the form Some S are not P. Now, replace ‘Democrats’ with ‘non-Democrats’, stick it in the predicate slot, and we get ‘Some politicians are not non-Democrats’. Well, that’s not exactly grammatically elegant, but the meaning is clear: not being a non-Democrat is just being a Democrat. This says the same are the original, namely that some politicians are Democrats.
Finally, particular negative, O. We’ll try ‘Some plants are not flowers’. Changing from negative to affirmative means our obverse will be an I—Some S are P. We replace ‘flowers’ with ‘non-flowers’ and get ‘Some plants are non-flowers’. We went from ‘Some plants are not flowers’ to ‘Some plants are non-flowers’. Obviously, those are equivalent.
Summary for obversion: obverses are equivalent for A, E, I, and O.
Contraposition
Our last operation is contraposition. Unlike obversion, and like conversion, it doesn’t involve changing the type (A, E, I, O) of the sentence we’re operating on. Rather, again, like conversion, we just manipulate the subject and predicate. Here’s how: replace the subject with the complement of the predicate; and replace the predicate with the complement of the subject. The result of performing contraposition on a sentence is called its contrapositive.
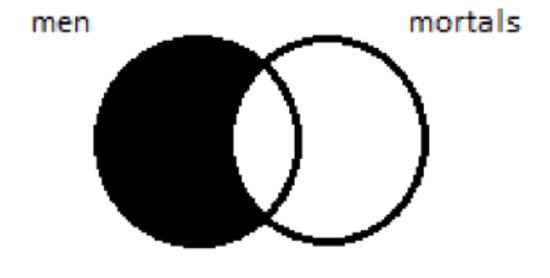
Let’s perform contraposition on an A sentence: ‘All men are mortals’. To form its contrapositive, we put the complement of the predicate—non-mortals—into subject position and the complement of the subject—non-men—into predicate position: ‘All non-mortals are non-men’. The question, as always: are these sentences equivalent? This one’s a bit hard to see. Let’s use Venn diagrams to help us think it through. First, we know what the diagram for ‘All men are mortals’ looks like; that sentence claims that there’s no such thing as a man who’s not a mortal, so we blot out the portion of the ‘men’ circle that’s not inside the ‘mortals’ circle:
Next, let’s think through how we would diagram ‘All non-mortals are non-men’. If we change our circles to ‘non-men’ and ‘non-mortals’, respectively, it’s easy; when you’re diagramming an A proposition, you just blot out the part of the left-hand (subject) circle that doesn’t overlap with the right-hand (predicate) circle. There’s no such thing as non-men who aren’t non-mortals:
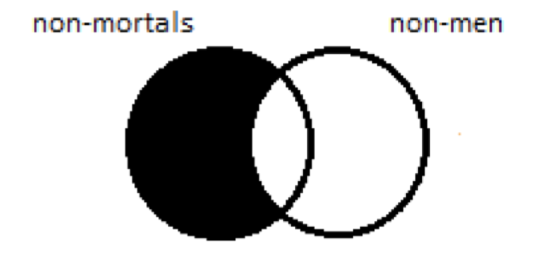
But how do we compare this diagram with the one for ‘All men are mortals’ to see if they express the same proposition? We need to know that the two would give us the same picture if the circles were labeled the same.
Let’s compare the unshaded diagrams where the circles are ‘men’ and ‘mortals’, on the one hand, and ‘non-men’ and ‘non-mortals’ on the other:

When we depict ‘All men are mortals’, we blot out region 1 of the left-hand diagram. When we depict its contrapositive, ‘All non-mortals are non-men’, we blot out region w of the right-hand diagram. We want to know whether these two sentences are equivalent. They are, provided that blotting out region 1 and blotting out region w amount to the same thing. Do they? That is, do regions 1 and w contain the same objects?
Let’s think this through, starting with region z. What’s in there? Those are the things that are outside both the non-mortal and non-men circles; that is, they’re not non-mortals and they’re not non-men. So they’re mortals and men, right? Things that are both mortals and men: on the left- hand diagram, that’s the overlap between the circles. Region z and region 2 contain the same things.
How about region y? Those things are non-men, but they’re outside the non-mortals circle, making them mortals. Mortals who aren’t men: they live in region 3 in the left-hand diagram. Regions y and 3 contain the same things. Region x has things that are both non-men and non-mortals; that is, they’re outside both the mortal and men circles on the left. Regions x and 4 contain the same things.
And region w? Outside the non-men circle, so they’re men. Inside the non-mortals circle, so they’re not mortals. Men that aren’t mortals: that’s region 1 on the left. Regions w and 1 contain the same things. And that means that blotting out region w and blotting out region 1 amount to the same thing; both are ways of ruling out the existence of the same group of objects, the men who aren’t mortals—or, as it turns out, the non-mortals who aren’t non-men. Same thing.
Picking the main thread back up, what all this shows is that when we perform contraposition on universal affirmative, A sentences, we end up with new sentences that express the same proposition. An A sentence and its contrapositive are equivalent. We still have to ask the same question about E, I, and O sentences.
Consider a universal negative (E): ‘No sky-divers are cowards’. This is surely true; it takes bravery to jump out of a plane (I wouldn’t do it). To get the contrapositive, we replace the subject, skydivers, with the complement of the predicate, non-cowards; and we replace the predicate, cowards, with the complement of the subject, non-sky-divers. The result is ‘No non-cowards are non-skydivers’. That’s false. You know who was a non-coward? Martin Luther King, Jr. The Reverend King was a courageous advocate for racial equality up to the very last day of his life. (If you need proof, watch his final speech, given the night before he was shot, in Memphis. The stirring finish: “So I’m happy tonight. I’m not worried about anything. I’m not fearing any man. Mine eyes have seen the glory of the coming of the Lord!” Just watch it; trust me. Amazing) But, not a sky-diver. The contrapositive claims there’s no such thing as a non-coward who doesn’t sky-dive. But that ain’t so: MLK is a counterexample. In general, when you perform contraposition on an E sentence, you end up with a new sentence that expresses a different proposition. And as was the case with A and O sentences being converted, this has unpredictable effects on truth-value. You may move from truth to falsehood, as in this case, or from truth to truth, falsehood to falsehood, falsehood to truth. Contraposition changes the proposition expressed by E sentences, so you can’t know.
Next, consider particular negative (O) sentences. These are pretty easy. ‘Some men are not priests’ is a good go-to example. Performing contraposition, we get ‘Some non-priests are not non-men’. Things that are not non-men—those are just men. So the claim being made by the contrapositive is that some non-priests are men. That is, there’s at least one thing that’s both a non-priest and a man; or, there’s at least one man who’s not a priest. I know a way to say that: ‘Some men are not priests’. The O sentence and its contrapositive make the same claim. Contraposition performed on particular negatives gives you a new sentence that is equivalent to the original.
Finally, particular affirmatives—I sentences. ‘Some men are priests’ is true. So is its contrapositive: ‘Some non-priests are non-men’ (there’s at least one: my mom is not a man, nor was she ever a priest). So contraposition performed on an I works? That is, it gives you an equivalent sentence? Not necessarily. The two sentences might both be true, but they could be expressing two different true propositions. As a matter of fact, they are. When you contrapose an I sentence, the result is a new sentence that is not equivalent. To see why, we’ll return to Venn diagrams.
Generically speaking, an I proposition’s diagram has an X in the area of overlap between the two circles. For a sentence of the form Some S are P, we would draw this.
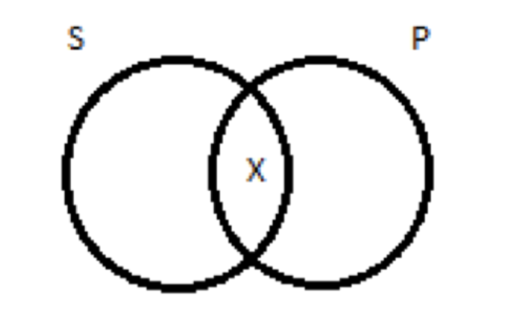
There is at least one thing (the X) that is both S and P. For the contrapositive, we draw this:
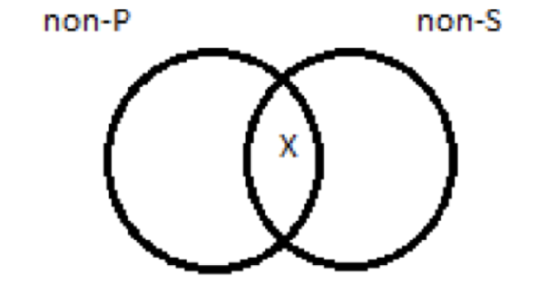
There is at least one thing that is both non-P and non-S. The question is, does drawing an X in those two regions of overlap amount to the same thing? Let’s put the diagrams side-by-side, without the Xs, but with numbers and letters for the different regions:
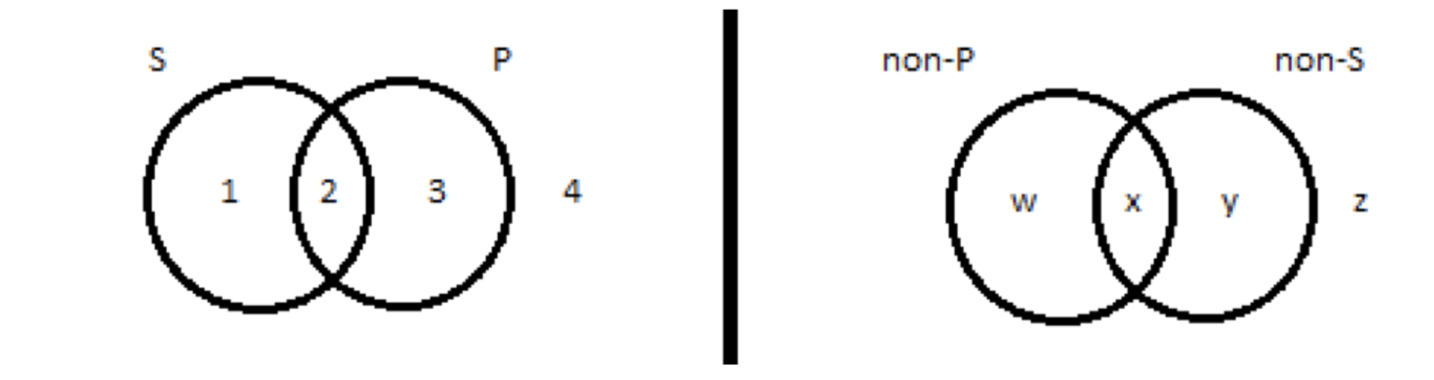
We went through this above when we were discussing the effects of contraposition on A propositions. Regions 1 and w contain the same things, as do regions 3 and y. But regions 2 and 4 don’t line up with regions x and z, respectively. Rather, they’re reversed: region 2 has the same objects as region z, and region 4 has the same objects as region x.
When we draw the picture of the straight-up I sentence, we put an X in region 2; when we draw the picture of its contrapositive, we put an X in region x. But region 2 and region x aren’t the same. So the I sentence and its contrapositive, in general, are not equivalent. Performing contraposition on an I sentence changes the proposition expressed, with unpredictable effects on truth-value.
We can prove it with a concrete example. Let our starting I sentence be ‘Some Catholics are non- Popes’. That’s certainly true (again, my mom: Catholic, but not Pope). The contrapositive would be ‘Some Popes are non-Catholics’ (the complement of non-Popes is just Popes). But that’s false. Being Catholic is a prerequisite for the Papacy. An I sentence and its contrapositive make different claims.
Exercises
1. Perform conversion on the following and write down the converse. Is it equivalent to the original sentence?
(a) Some surfers are not priests.
(b) All Canadians are bodybuilders.
(c) No Mexicans are fishermen.
(d) Some Nazis are florists.
2. Perform obversion on the following and write down the obverse. Is it equivalent to the original sentence?
(a) No people are lizards.
(b) Some politicians are criminals.
(c) Some birds are not animals.
(d) All Democrats are samurais.
3. Perform contraposition on the following and write down the contrapositive. Is it equivalent to the original sentence?
(a) All Philistines are Syrians.
(b) No Africans are Europeans.
(c) Some Americans are Irishmen.
(d) Some Swiss are not Catholics.
Inferences
Earlier, we discussed how we could make inferences about the truth-values of categoricals using the information encoded in the Square of Opposition. For example, given the supposition that an A sentence expresses a true proposition, we can infer that the corresponding E sentence expresses a falsehood (since A and E are contraries, which can’t both be true), that the corresponding I sentence expresses a truth (since I is the subaltern of A, which means A’s truth guarantees that of I), and that the corresponding O sentence expresses a falsehood (since A and O are contradictories, which must have opposite truth-values).
The keyword in that paragraph is ‘corresponding’. The Square of Opposition tells us about the relationships among categoricals that correspond—which means they have the same subjects and predicates. If ‘All S are P’ is true, then ‘No S are P’ must be false, per the Square, since these two sentences have the same subject (S) and predicate (P). The square cannot license such inferences when the subjects and predicates do not correspond. The supposition that ‘All S are P’ is true tells me nothing at all about the truth-value of ‘Some A are B’; the subjects and predicates are different; we’re dealing with two different classes.
There are occasions, however, when subjects and predicates do not correspond, but we can nevertheless make inferences about the truth-values of categoricals based on information about others. In such cases, we need to combine our knowledge of the relationships depicted in the Square of Opposition with our recently acquired knowledge about the circumstances in which conversion, obversion, and contraposition provide us with equivalent sentences.
Here is a simple example. Suppose that a sentence of the form ‘No S are P’ expresses a truth (never mind what ‘S’ and ‘P’ stand for; we’re thinking in the abstract here). Given that information, what can we say about a sentence of the form ‘Some P are S’? Well, the first is an E and the second is an I. According to the Square of Opposition, E and I are a contradictory pair, so they must have opposite truth-values. But remember, the relationships in the Square only hold for corresponding sentences. ‘No S are P’ and ‘Some P are S’ do not correspond; their subject and predicate class terms are in different spots. The Square tells us that the I sentence corresponding to ‘No S are P’— namely, ‘Some S are P’—must be the opposite truth-value. We’ve presumed that the E sentence is true, so ‘Some S are P’ expresses a falsehood, according to the Square. But we wanted to know the truth-value of ‘Some P are S’, the sentence with the subject and predicate terms switched. Well, switched subject and predicate terms—that’s just the converse of ‘Some S are P’. And we know from our investigations that performing conversion on an I sentence always gives you another I sentence that’s equivalent to the first; that is, it expresses the same proposition, so it’s true or false in all the same circumstances as the original. That means ‘Some P are S’ must express a falsehood, just like its converse.
Here’s how to think about the inference we just made. We were given the fact that ‘No S are P’ is true. We wanted to know the truth-value of ‘Some P are S’. (We’re getting a little sloppy here. Technically, it’s propositions, not sentences, that are true or false. Further complication: we’re not even talking about actual sentences here, but generic sentence-patterns, with placeholder letters ‘S’ and ‘P’ standing in for actual class terms. Can those sorts of things be true or false? Ugh. Let’s just agree not to be fussy and not to worry about it. We all understand what’s going on) We can’t compare these two directly using the Square of Opposition because they don’t correspond: different subject and predicate. But, we know that the converse of the our target sentence—‘Some S are P’—does correspond, so according to the Square, it must be false (since it’s contradictory to ‘No S are P’). And, since conversion on I sentences yields equivalent results, ‘Some P are S’ has the same truth-value as ‘Some S are P’, so our target sentence must also be false.
This is the general pattern for these sorts of multi-step inferences. You’re given information about a particular categorical claim’s truth-value, then asked to evaluate some other claim for truth or falsity. They may not correspond, so the first stage of your deliberations involves getting them to correspond—making the subject and predicate terms line up. You do this by performing conversion, obversion, and contraposition as needed, but only when those operations produce equivalent results: you only use conversion on E and I sentences; you only use contraposition on A and O sentences; and since obversion always yields an equivalent sentence, you can use it whenever you want. Then, once you’ve achieved correspondence, you can consult the Square of Opposition and complete the inference.
Another example can help illustrate the method. Suppose we’re told that some sentence ‘All S are P’ is true. What about the sentence ‘No ~ S are ~ P’? (Remember, when we put the tildes in front of the letters, we’re referring to the complements of these classes.)
First, we notice that the subject and predicate terms don’t correspond. The A sentence has ‘S’ in subject position and ‘P’ in predicate position, while the target E sentence has ~ S and ~ P in those slots. We can see this misalignment clearly (and also set ourselves up more easily to think through the remaining steps in the inference) if we write the sentences out, one above the other (noting in brackets what we know about their truth-values):
All S are P [T]
No ~ S are ~ P [?]
Focusing only on subject and predicate terms, we see that the bottom ones have tildes, the top ones don’t. We need to get them into correspondence. How? Well, it occurs to me that we have an operation that allows us to add or remove tildes, two at a time: contraposition. When we perform that operation, we replace the subject with the complement of the predicate (adding or removing one tilde) and we replace the predicate with the complement of the subject (adding or removing another). Now, contraposition produces equivalent sentences for A and O, but not E and I. So I can only perform it on the top sentence, ‘All S are P’. Doing so, I produce a contrapositive which expresses the same proposition, and so must also be true. We can write it down like this:
All S are P [T]
All ~ P are ~ S [T]
No ~ S are ~ P [?]
The sentence we just wrote down still doesn’t align with the target sentence at the bottom, but it’s closer: they both have tildes in front of ‘S’ and ‘P’. Now the problem is that the ‘~ S’ and ‘~ P’ are in the wrong order: subject and predicate positions, respectively, in the target sentence, but the reverse in the sentence we just wrote down. We have an operation to fix that! It’s called conversion: to perform it, you switch the order of subject and predicate terms. The thing is, it only works— that is, gives you an equivalent result—on E and I sentences. I can’t perform conversion on the A sentence ‘All ~ P are ~ S’ that I just wrote down at the top. But, I can perform it on the target E sentence at the bottom:
All S are P [T]
All ~ P are ~ S [T]
No ~ P are ~ S [?]
No ~ S are ~ P [?]
I did conversion, as it were, from the bottom up. Those last two E sentences are converses of one another, so they express the same proposition and will have the same truth value. If I can figure out the truth-value of ‘No ~ P are ~ S’, then I can figure out the truth-value of my target sentence on the bottom; it’ll be the same. And look! I’m finally in a position to do that. The two sentences in the middle, ‘All ~ P are ~ S’ and ‘No ~ P are ~ S’, correspond; they have the same subject and predicate. That means I can consult the Square of Opposition. I have an A sentence that’s true. What about the corresponding E sentence? They’re contraries, so it must be false:
All S are P [T]
All ~ P are ~ S [T]
No ~ P are ~ S [F]
No ~ S are ~ P [?]
And since the target sentence at the bottom expresses the same proposition as the one directly above it, that final question mark can also be replaced by an ‘F’. Inference made, problem solved.
Again, this is the general pattern for making these kinds of inferences: achieve correspondence by using the three operations, then use the information encoded in the Square of Opposition.
This works most of the time, but not always. Suppose you’re told that ‘All S are P’ is true, and asked to infer the truth-value of ‘No P are ~ S’. We can again write them out one above the other and take a look:
All S are P [T]
No P are ~ S [?]
‘S’ and ‘P’ are in the wrong order, plus ‘S’ has a tilde in front of it on the bottom but not on the top. The first thing that occurs to me to do is to get rid of that tilde. We have an operation for adding or removing one tilde at a time: obversion. I’m going to perform it on the bottom sentence. First, I change the quality: the universal negative (E) original becomes a universal affirmative (A). Then I replace the predicate with its complement: I replace ‘~ S’ with just plain ‘S’. This is the result:
All S are P [T]
All P are S [?]
No P are ~ S [?]
We don’t have correspondence yet, but we’re closer with that tilde out of the way. What next? Well, now the problem is just that ‘S’ and ‘P’ are in the wrong order. There’s an operation for that: conversion. But—and here’s the rub—we can only use conversion on E and I sentences. Now that I did obversion on the target at the bottom, the two sentences I’m left comparing are both As. I can’t use conversion on an A: the result won’t be equivalent.
At this point, the sensible thing to do would be to try other operations: maybe the right combination of obversion, contraposition, and possibly, eventually, on a different kind of sentence, conversion, will allow us to achieve correspondence. When making these kinds of inferences, you often have to try a variety of things before you get there. But I’m here to tell you, try what you might in this example, as many conversions, obversions, and contrapositions as you want, in whatever order: you’ll never achieve correspondence. It’s impossible.
So what does that mean? It means that, given the fact that ‘All S are P’ is true, you cannot make any inference about the truth-value of ‘No P are ~ S’. The answer to the problem is: “I don’t know.” Remember, this kind of thing can happen; sometimes we can’t make inferences about one categorical based on information about another. When we know that an I is true, for example, we can’t say what the truth-value of the corresponding O is; it could go either way.
That’s kind of unsatisfying, though. I’m telling you that if you can’t achieve correspondence—if it’s impossible—that you can’t make an inference. But how do you know that you can’t achieve correspondence? Maybe, as you were laboring over the problem, you just didn’t stumble on the right combination of operations in the right order. How do we know for sure that an inference can’t be made? As a matter of fact, the one step that we took in this problem puts us in a position to know just that. Compare ‘All S are P’ with the obverse of the target sentence, ‘All P are S’. What’s the relationship between those? One is the converse of the other. We’re given a true A sentence, and asked to make an inference about the truth-value of a sentence equivalent to its converse. But performing conversion on an A, as we established at length above, gives you a new sentence that expresses a different proposition. And this has unpredictable effects on truth-value: sometimes one goes from truth to falsity; other times from truth to truth, and so on. In this case, we know that we can’t know the truth-value of the target sentence, because it’s equivalent to the result of perform conversion on a universal affirmative, and the effects of that operation on truth-value are unpredictable.
In general, you can know that the answer to one of these problems is “I don’t know” if you can use the operations to get into a position where you’re comparing a sentence with its converse or contrapositive when those operations don’t work for the types of sentences you have. We saw this for an A and its converse. Similarly, if you have an E sentence of known truth-value, and your target sentence is equivalent to its contrapositive, you know the answer is “I don’t know,” because contraposition performed on E sentences has unpredictable results on truth-value. Same goes for I and conversion, O and contraposition.
Exercises
1. Suppose ‘All S are P’ is true. Determine the truth-values of the following (if possible).
(a) No S are ~ P
(b) All ~S are ~ P
(c) No ~ P are S
(d) Some ~ P are S
(e) Some ~ S are not ~ P
2. Suppose ‘No S are P’ is true. Determine the truth-values of the following (if possible).
(a) Some ~ P are not ~ S
(b) All ~ S are ~ P
(c) No ~ S are ~ P
(d) Some ~ P are S
(e) All ~ P are ~ S
3. Suppose ‘Some S are P’ is true. Determine the truth-values of the following (if possible).
(a) All S are ~ P
(b) Some S are not ~ P (c) No P are S
(d) Some P are ~ S
(e) No S are ~ P
4. Suppose ‘Some S are not P’ is true. Determine the truth-values of the following (if possible).
(a) No S are ~ P
(b) Some S are ~ P
(c) No ~ S are P
(d) No ~ P are S
(e) Some P are S


