2.14: Categorical Logic
- Page ID
- 27932
Consider the following argument:
- All humans are mortal
- All mortal things die
- Therefore, all humans die
If we were to apply the informal test of validity (from chapter 1) to this argument, we would see that the argument is valid because it is not possible to imagine a scenario in which the premises are true and yet the conclusion is false. However, look at what happens if we try to translate it using propositional logic. Since “all humans are mortal” is atomic, (i.e., it does not contain any truth functional operators) we can translate it using the constant “H.” The second premise, “all mortal things die,” is also atomic, so we can translate it using the constant, “M.” Finally, the conclusion, is yet another atomic statement, “All humans die,” which we can translate “D.” But then the form of our argument is just this:
- H
- M
- ∴ D
The problem is that this argument is not valid, which we can clearly see by constructing a truth table. Since there are three different atomic components, our truth table will be 8 rows. (In the following truth table, since the reference columns would just be identical to the premise and conclusion columns, I just collapsed the two in order to make the truth table less redundant.)
| H | M | D |
|---|---|---|
| T | T | T |
| T | T | F |
| T | F | T |
| T | F | F |
| F | T | T |
| F | T | F |
| F | F | T |
| F | F | F |
Notice the second row of the truth table (which I have bolded). The premises are both true on that row and yet the conclusion is false. That means that this argument does not pass the truth table test of validity and so is invalid. But clearly this argument is valid. If it is true that all humans are mortal and that all mortal things die, then it must be true that all humans die. What this argument reveals is one of the limitations of propositional logic. There are some arguments that are intuitively valid (such as this one) but that cannot be shown to be valid using the methods of propositional logic. This shows that we need other kinds of formal logic to be able to capture a wider range of logically valid inferences. Categorical logic allows us to supplement propositional logic with a formal method that will handle arguments like this that propositional logic is unable to handle.
Categorical logic is the logic that deals with the logical relationship between categorical statements. A categorical statement is simply a statement about a category or type of thing. For example, the first premise of the above argument is a statement about the categories of humans and things that are mortal. The second premise is a statement about the categories of things that are mortal and things that die. Finally, the conclusion is a statement about humans and things that die. Although you may think that this argument as a similar form as a hypothetical syllogism, it is distinct from a hypothetical syllogism because the premises are not composed of two different atomic propositions. Rather, each premise contains only one atomic proposition.
In categorical logic, the logical terms (analogous to the truth functional operators of propositional logic) are the terms “all” and “some.” In contrast with propositional logic, in categorical logic we will use capital letters to stand for categories of things in the world, rather than for atomic propositions. Thus, we can represent the statement:
All humans are mortal
as
All H are M
where “H” stands for the category of “humans” and “M” stands for the category, “things that are mortal.” Notice that the categories are nouns or noun phrases. Thus, instead of saying that the category is “mortal” I said the category is “things that are mortal.” It is important to recognize the difference between how the capital letters are being used in categorical logic and how they were used in propositional logic. In categorical logic, the capital letters stand for noun phrases that denote categories of things in the world—for example, “cars” or “things that are man-made” or “mammals” or “things that are red.”
In categorical logic, we will use what are called Venn diagrams to represent the logical relationships between the different kinds of categorical statements. A Venn diagram is simply a way of graphically representing the logical relationship between two different categorical statements. Below is a Venn diagram that represents the statement, “all humans are mortal.”
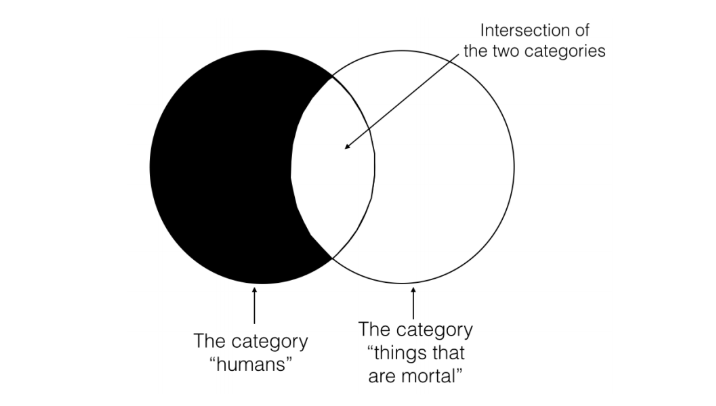
Here is how to understand this Venn. There are two circles that represent the two categories, “humans” and “things that are mortal.” These two categories are overlapping so that the intersection of those two categories (i.e. the place where the two circles overlap) represents things that are both human and mortal. Any shaded portions of the Venn diagram (by “shaded” I will mean “blacked out”) represent that there is nothing in that area of the category. So the above Venn says that there is nothing in the category “humans” that is not also in the category “things that are mortal.” The above Venn also allows that there are things that are in the category “things that are mortal” but that aren’t in the category “humans” (which is as it should be since, of course, dogs are mortal and yet not human). So the reason the category “things that are mortal” is left unshaded is that in saying “all humans are mortal” I leave open the possibility that there are things that are not human and yet mortal.
As noted above, the statement, “all humans are mortal,” has a particular form:
All H are M.
This is one of the four categorical forms. The way we will represent these categorical forms generally are with an “S” (which stands for “subject term”) and a “P” (which stands for “predicate term”). Thus, the categorical statement, “all humans are mortal,” has the following categorical form:
All S are P
The way we interpret statements of this form are as follows: everything in the category S is also in the category P. This statement form is what we call a “universal affirmative,” since it is a universal statement that does not contain a negation. There are three other categorical statement forms that you will have to become familiar with in order to do categorical logic. Here they are (with the name of the type of statement in parentheses to the right:
No S are P (universal negative)
Some S are P (particular affirmative)
Some S are not P (particular negative)
Here are three examples of statements that have these three forms (respectively):
No reptiles give live birth
Some birds are taller than President Obama
Some birds don’t fly
Notice that although these three statements don’t have exactly the same form as the statement forms above, they can be translated into those same forms. All we have to do is figure out the noun phrase that describes each category that the statement is referring to. Let’s start with “no reptiles give live birth.” This categorical statement refers to two different categories: the category of “reptiles” and the category of “things that give live birth.” Notice, again, that I added “things that...” to the predicate of the sentence (“give live birth”) because “give live birth” is not a description of a category. Rather, the way of describing the category is with the noun phrase, “things that give live birth.” Using these two category descriptions, we can translate this sentence to have the same form as its categorical form. All we have to do is substitute in the name of the subject category (i.e., the “S” term) and the description of the predicate category (i.e., the “P” term). Doing that will yield the following sentence:
No reptiles are things that give live birth
Although this sentence sounds strange in English, it has the same form as the categorical form, no S are P, and this translation allows us to clearly see that it does and thus to see what the two categories are. Here is what the Venn diagram for this statement looks like:
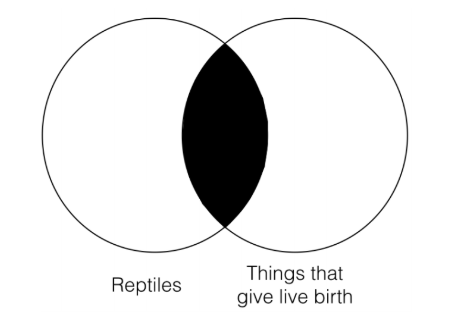
This Venn diagram represents that there is nothing in the intersection of the two categories, “reptiles” and “things that give live birth.” If you think about it, this is exactly what our original statement was saying: there isn’t anything that is both a reptile and gives live birth.
Let’s look at the next statement, “some birds are taller than President Obama.” This is a statement not about all birds, but about some birds. What are the two categories? One category is clearly “birds.” The other category is “things that are taller than President Obama.” That may sound like a strange category, but it is perfectly legitimate category. It includes things like adult ostriches, large grizzly bears standing on their hind legs, giraffes, the Flatiron Building, a school bus, etc. Here is how we’d translate this sentence using our two categories: Some birds are things that are taller than President Obama. Again, although this sentence sounds strange in English, it has the same form as the categorical form, some S are P, and it allows us to clearly see what the two categories are. Below is the Venn diagram for this statement:

By convention, an asterisk on the Venn diagram means that there is at least one thing in that category. By putting the asterisk in the intersection of the two categories, we are saying that there is at least one thing that is a bird and is taller than President Obama, which is exactly what our original sentence was saying.
Finally, let’s consider the statement, “some birds don’t fly.” How would we translate this sentence to have the “some S are not P” form? The first step is to get the descriptions of the two categories using either nouns or noun phrases.
The “S” term is easy; it is just “birds” again. But we have to be a bit more careful with the “P” term, since its predicate contains a negation. We do not want any of our categories to contain a negation. Rather, the negation is contained in the form (i.e., the “not”). The category cannot be simply “fly” or even “flies” since neither of these are a category of thing. We have to use our trick of turning the predicate into a noun phrase, i.e., “things that fly.” Given these two category descriptions, we can then translate the sentence to have the categorical form, some S are not P:
Some birds are not things that fly
Again, although the English sounds clunky here, it has the same form as the categorical form, some S are not P, and it allows us to clearly see what the two categories are. Below is the Venn diagram for this statement:
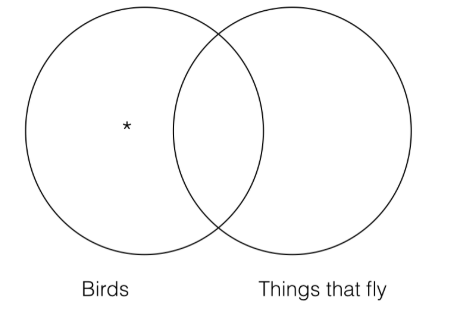
By convention, an asterisk on the Venn diagram means that there is at least one thing in that category. By putting the asterisk inside the “birds” category, but outside the “things that fly” category, we are representing that at least one thing that is a bird isn’t a thing that flies. This is exactly what our original sentence was saying.
Translating categorical statements into their categorical form can by tricky. In fact, it is probably one of the trickier things you’ll do in formal logic. There is no simple way of doing it other than asking yourself whether your translation accurately captures the meaning of the original English sentence. Here is an example of a tricky categorical statement:
Nobody loves me but my mother.
This is a categorical statement, but which of the four categorical forms does it have? The first step is to ask what two categories are being referred to in this sentence. Here are the two categories: “things that love me” and “things that are my mother.” Notice that the category couldn’t just be “my mother” since that isn’t a category; it’s a particular thing. Again, this sounds strange, but it is important to remember that we are describing categories of things. The next question is: what is this sentence saying is the relationship between these two categories? Hint: it has to be one of the four categorical forms (since any categorical statement can be translated into one of these four forms). The sentence is saying that the only things that love me are things that are my mother. The categorical form of the statement is the “all S are P” form. Thus, the sentence, translated into the correct categorical form would be:
All things that love me are things that are my mother.
We will end this section with one last example. Consider the following categorical statement:
The baboon is a fearsome beast.
Which of the four categorical forms does this statement have? Although the article “the,” which often denotes particulars, may lead one to think that this is a particular affirmative form (some S are P), it is actually a universal affirmative form (all S are P). This English sentence has the sense of “baboons are fearsome beasts” rather than of “that (particular) baboon is a fearsome beast.” English is strange, which is what makes translation one of the trickiest parts of logic. So, the two categories are: “baboons” and “fearsome beasts.” Notice that since “fearsome beasts” is already a noun phrase, we don’t have to add “things that are...” to it. Using the two category descriptions, the translation into the “all S are P” categorical form is thus:
All baboons are fearsome beasts.
In this section we have learned what categorical statement are, how to translate categorical statements into one of the four categorical forms, and how to construct Venn diagrams for each of the four categorical forms. The following exercises will give you some practice with the translation part; in subsequent sections we will learn how to use Venn diagrams as a formal method of evaluating a certain class of arguments.
Exercise
Translate each of the following sentences into one of the four categorical forms (universal affirmative, universal negative, particular affirmative, particular negative). Make sure that the descriptions of the two categories are nouns or noun phrases (rather than adjectives or verbs).
1. Real men wear pink.
2. Dinosaurs are not birds.
3. Birds evolved from dinosaurs.
4. Some mammals are not predators.
5. Some predators are not mammals.
6. Not all who wander are lost.
7. All presidents are not women.
8. Boxers aren’t rich.
9. If someone is sleeping then they aren’t conscious.
10. If someone is conscious then they aren’t sleeping.
11. All’s well that ends well.
12. My friends are the only ones that care.
13. Someone loves you.
14. Jesus loves everyone.
15. Jesus loves the little children.
16. Some people don’t love Jesus.
17. Only pedestrians may use the Appalachian Trail.
18. Only citizens can be president.
19. Anyone who is a Hindu believes in God.
20. Anything that is cheap is no good.
21. Some expensive things are no good.
22. Not all mammals have legs.
23. There are couples without children.
24. There are no people who hate chocolate.
25. There are people who hate cats.
26. Nothing that is sharp is safe.
27. No poodle could run faster than a cheetah.
28. No professional runner is slow.
29. Baboons aren’t friendly.
30. Pigs will eat anything.


