4.2: Quickly Recognizing Simple Intervals

Last updated
Save as PDF

Page ID: 52038

Terry B. Ewell & Catherine Schmidt-Jones
Connections

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Musicians need to be able to quickly recognize intervals in printed music. Counting intervals by half steps is often too slow, particularly with intervals greater than thirds. This module introduces a method that can greatly increase facility with interval recognition.

(This module assumes that you understand how to assign interval numbers and quality. Please see “Interval” by Katherine Schmidt-Jones, module m10867, for further reference)

A thorough knowledge of major scales is central to rapid identification of intervals. The quality of the interval between each scale step and the tonic is either major or perfect (Figure 1)

In particular, intervals up to a perfect 5^th can be quickly recognized through knowledge of the major scales. Scale steps are used as quick reference points with which to compare the intervals. Let’s look at some examples to explain how this works.

In Figure 2, consider the lowest pitch the tonic note of B major. Knowing that B major has a C# in the scale indicates to us that C natural is not a major 2^nd above B. Since C is a half step below C# the interval is therefore a minor 2^nd.

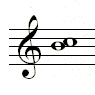
In Figure 3, a D major scale has two sharps, one of which is F#. Since F natural is half a step below F# it must be a minor third above D.

In Figure 4, A major has F#, C#, and G# but no D#. D natural is a perfect 4^th above A; therefore D# must be an augmented 4^th above A.

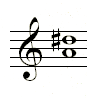
In Figure 5, F major has one flat-Bb. Bb is therefore a perfect fourth above F.

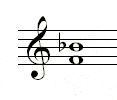
In Figure 6, a B major scale requires an F#. F natural, being half a step lower, is a diminished fifth above B.

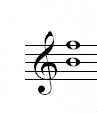
Other “Tricks’

I find classifying intervals of sixths or sevenths more problematic with scales. I often double check my answers by inverting the intervals. For instance in Figure 7, it is not easy for me to quickly recognize the interval D# to B, but B to D# can be quickly recognized. Rules of inversion indicate that a major 3^rd inverts to a minor 6^th.

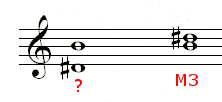
Likewise the seventh in Figure 8 is easier to recognize as a second:

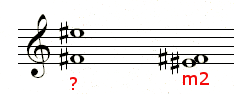
Figure 8 illustrates a further “trick.” Since both notes are preceded by sharps, one can ignore the sharps and consider the interval to be the same as E to F. This is easier to recognize E to F as a minor second than E# to F#. One may do the same operation if both notes bear flats; consider the interval without the flats present.