12.6: Exercises
- Page ID
- 22039
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)■ 1. Find three classes in the real world that have the relationships indicated in the following diag r am:
2. Draw a diagram in which the following statement is true, and draw one in which it is false: "Only non-handheld things are returnable." Be sure to define your labels.
■ 3. Draw a diagram in which it is true that although no Americans are voters, some of them are free and some aren't, yet all of them are rich. In your diagram, are all the voters rich?
4. If all A are C but no C are B, then are some A also B?
■ 5. Finding something that has both properties W and T tends to confirm the statement "All W are T"; for example, finding a black raven tends to confirm the statement "All ravens are black."
a. true
b. false
6. If all non-black things are non-ravens, then you can be sure there are no albino ravens.
a. true
b. false
7. Assuming that all non-black things are non-ravitious, it follows with certainty that all nonravitious things are non-black.
a. true
b. false
8. Even if all ravens are black, it would not necessarily be the case that everything that is not black fails to be a raven.
a. true
b. false
9. The sentence can be used to express an invalid argument. Turn it into a deductively valid argument by adding the word only.
Children pay no taxes at all, because children are not adults and because adults pay taxes.
■ 10. Give the logical form of the following argument in class logic. Define your new symbols, but let M = the class of modern works of art. Draw the relevant diagrams for assessing the deductive validity of the argument. Assess its validity by referring to your diagram(s): that is, say, "These diagrams show that the argument is valid (or invalid) because..."
Since all modern works of art are profound works of art, but not all profound works of art are modern works of art, and because some religious works of art are modern works of art, even though some aren't, it follows that some religious works of art fail to be profound.
■ 11. The Venn-Euler diagram technique is a way of testing whether something is wrong (invalid) with the pattern of arguments that are about classes of things.
a. true
b. false
12. Given a class logic argument that is deductively valid but unsound, the diagram technique can show why it is unsound.
a. true
b. false
13. Use the method of diagrams to determine the validity or invalidity of the following argument:
There are doctors who aren't rich, because all doctors are professionals, yet some professionals are not rich.
14. If no items from column C are nondeductible, and if column C is not empty of items, then can we infer with certainty that at least one item from column C is deductible?
■ 15. Is this argument deductively valid?
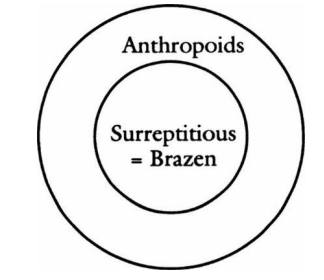
Some anthropoids are surreptitious and some aren't; hence there are brazen things that aren't anthropoids because all surreptitious beings are brazen.
■16. Is this argument deductively valid? Use the method of diagrams, and show your work.
There are prize winners who aren't avaricious, because every early entrant is a prize winner and because one or more avaricious beings did enter early, though some didn't.
17. Is this argument deductively valid? Use the method of diagrams, and show your work.
There are prize winners who aren't avaricious, because all early entrants are prize winners and some avaricious persons entered early and some early entrants aren't avaricious.
18. Is the statement "Some Arabs are Dravidians" true in the following diagram?
a. yes
b. no
19. Is this argument deductively valid? First, consider whether the argument is best handled with sentential logic or class logic.
The moon maidens don't like Miller Lite. If the Beast controls planet Gorp, then Xenon is in power on that moon. If Xenon is in power on that moon, then the moon maidens like Miller Lite. So the Beast doesn't control planet Gorp.
Give the logical form of the argument. Define your terms.
20. One of the following two arguments is deductively valid, and the other is not. Identify the invalid one, and use the method of Venn-Euler diagramming to defend your answer.
A = Arabs D = Dravidians
- There are biopical persons who aren't devious because some devious persons are not surreptitious, and some are, and because a person is surreptitious only if he or she is biopical.
- There are biopical persons who aren't devious because some surreptitious persons are not devious, and some are, and because any person is biopical if he or she is surreptitious.
21. Use the technique of diagrams to assess the validity of the following arguments:
a. If some A are C, and all C are R, then some R must be A
b. No A are B.
Some B are C.
So, no A are C.
c. No A are B.
All B are C.
So, no A are C.
22. Which diagram demonstrates the deductive invalidity of the following argument?
No apes are bears.
No bears are cats.
So, no apes are cats.
23. Draw a diagram that will demonstrate the deductive invalidity of the following argument that might be given by a political liberal who isn’t reasoning logically:
No conservatives in Congress are for helping humanity, because all supporters of legislation to increase welfare programs want to help humanity, yet none of the conservatives support legislation to increase welfare programs.
24. Are the following statements logically consistent with each other? Use diagrams to defend your answer.
Not only are no bluejays arachnids, but no dialyds are either. Still, some bluejays are catalytic, but not all are. Anything catalytic is a dialyd.
■ 25. To say that all the people who go to this restaurant are kids is to say something logically equivalent to
a. Only the people who go to this restaurant are kids.
b. Only kids (are the people who) go to this restaurant.
c. Neither a nor b.
d. Both a and b.
■ 26. Which pairs of statement forms from the following list are logically equivalent to
each other? In answering, use only the lowercase letters, not the statement forms themselves.
a. No Aare B.
b. No B are A
c. All are not-B.
d. All not-B are A.
e. Only not -A are B.
27. Which pairs of statements from the following list are logically equivalent to each other? In answering, use only the letters, not the statements. Hint: Use Aristotelian logic.
a. Every hand-held thing is nonreturnable.
b. No returnable thing is hand-held.
c. All nonreturnable things are hand-held.
d. Only non-hand-held things are returnable.
e. No hand-held thing is returnable.
■ 28. Are these logically equivalent? If not, why not?
a. Not all profound works of art are modern.
b. Not all profound works of art are modern works of art.
29. During Ronald Reagan's presidency, the United States Attorney General Edwin Meese III criticized the Supreme Court's Miranda decision that spelled out the legal rights of accused persons that the police must respect. Meese said, "The thing is, you don't have many suspects who are innocent of a crime.... If a person is innocent of a crime, then he is not a suspect." One of the following statements is logically equivalent to what Meese said in his last sentence. That is, Meese said
a. If a person is not innocent of a crime, he is not a suspect.
b. No suspects in a crime are innocent.
c. No persons who are not innocent of a crime are suspects.
d. All suspects in crimes are innocent.
e. If a person is innocent of a crime, then he is not guilty of the crime.
■ 30. Let's try out some more terminology from everybody's friend, the United States Internal Revenue Service.
If no items from column C are deductible, then can we infer with certainty that no deductible items are from column C? How about vice versa? What can you conclude about whether the two statements are logically equivalent?
31. Sofa and couch are equivalent terms—that is, they are synonymous. Now consider the term weird. Is the term closer to being equivalent to unusual or instead to very unusual ? If someone disagreed with you about this, what could you do to prove the person wrong?
32. To say that only the people who go to this restaurant are kids is to say something logically equivalent to
a. All the people who go to this restaurant are kids.
b. All kids go to this restaurant.
c. Neither a nor b.
d. Both a and b.
■ 33. Suppose someone says, "Only kids go to Chuck E. Cheese restaurants."
i. Would the following sentence, if true, be a counterexample?
Some kids in Russia don't go to Chuck E. Cheese restaurants.
ii. How about this as a counterexample instead?
I'm an adult, not a kid, and I go to Chuck E. Cheese restaurants.
34. Consider this argument:
All cylinders contain petroleum, since each one has a blue top and only petroleum containers have blue tops.
Does it follow from the second premise that some things can have blue tops but not be petroleum containers?
Solutions
1 A = fruit, B = oranges, C = things that grow on trees.
3 There are many acceptable diagrams. The relationship between voters and rich people is not fixed by the sentence. Consequently, you have leeway about where the voters' region can go. It can go outside the rich area, it can intersect it, or it can be wholly within it—provided that the voter area is wholly separate from the American area. In the following diagram all the voters are rich, but this need not be true in other acceptable diagrams
5 Answer (a).
10 Although you weren't asked for the standard form, here it is:
All modern works of art are profound works of art.
Not all profound works of art are modern works of art.
Some religious works of art are modern works of art.
Some religious works of art are not modern works of art.
So, some religious works of art fail to be profound.
The logical form of the argument is:
All M are P.
Not all P are M.
Some R are M.
Some R are not M.
Therefore, some R are not P.
where we used these definitions:
M = (the class of) modern works of art
P = the profound works of art
R = religious works of art
"Not all P are M" means that not all members of P are members of M.
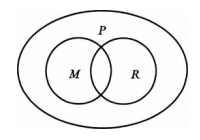
This diagram shows that the argument is deductively invalid because the diagram makes the premises (of the logical form) true while the conclusion is false.
11 Answer (a).
15 It is invalid because of the possibility of the situation shown in the following diagram:
16 To find the answer, translate it into the kind of English that more obviously talks about classes and that uses the terms all, some, and none in place of their equivalents.
All early entrants are prize winners.
Some avaricious beings are early entrants.
Some avaricious beings are not early entrants.
Some prize winners aren't avaricious.
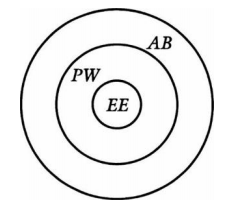
The logical form of the above is:
All EE are PW.
Some AB are EE.
Some AB are not EE.
Some PW are not AB.
Where
EE = (the class of) early entrants
PW = (the class of) prize winners
AB = (the class of) avaricious beings
Goal: To draw a diagram showing that the argument can have true premises while having a false conclusion—the sure sign of deductive invalidity. The diagram below achieves this goal:
25 Answer (b).
26 All pairs from the group {a, b, c, d} are logically equivalent.
28 Yes, they say the same thing, using the principle of charity. They are different grammatically but not logically. It is possible to interpret the first as meaning mean modern in time and the second as meaning modern in style. However, if you make the latter point, you should also notice that the two could be (better yet, are likely to be) logically equivalent; it is wrong to say they definitely are not equivalent. In fact, if the two sentences were used in a piece of reasoning and they did have different meanings, and if the context didn't make this clear, the reasoner would be accused of committing the fallacy of equivocation.
30 Yes. Yes. They are equivalent; they are two ways of saying the same thing.
33 i. no ii. yes


