1.6: Pythagoras
- Page ID
- 29873
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Pythagoras
Pythagoras of Samos was an Ionian Greek philosopher, mathematician, and the putative founder of the movement called Pythagoreanism. Most of the information about Pythagoras was written down centuries after he lived, so very little reliable information is known about him. He was born on the island of Samos, and travelled, visiting Egypt and Greece, and maybe India. Around 530 BC, he moved to Croton, in Magna Graecia, and there established some kind of school or guild. In 520 BC, he returned to Samos.
Pythagoras made influential contributions to philosophy and religion in the late 6th century BC. He is often revered as a great mathematician and scientist and is best known for the Pythagorean theorem which bears his name. However, because legend and obfuscation cloud his work even more than that of the other pre-Socratic philosophers, one can give only a tentative account of his teachings, and some have questioned whether he contributed much to mathematics or natural philosophy. Many of the accomplishments credited to Pythagoras may actually have been accomplishments of his colleagues and successors. Some accounts mention that the philosophy associated with Pythagoras was related to mathematics and that numbers were important. It was said that he was the first man to call himself a philosopher, or lover of wisdom, and Pythagorean ideas exercised a marked influence on Plato, and through him, all of Western philosophy.
Biographical sources
The stories which were created were eagerly sought by the Neoplatonist writers who provide most of the details about Pythagoras, but who were uncritical concerning anything which related to the gods or which was considered divine. Thus many myths were created – such as that Apollo was his father; that Pythagoras gleamed with a supernatural brightness; that he had a golden thigh; that Abaris came flying to him on a golden arrow; that he was seen in different places at the same time. According to Sir William Smith, with the exception of a few remarks by Xenophanes, Heraclitus, Herodotus, Plato, Aristotle, and Isocrates, we are mainly dependent on Diogenes Laërtius, Porphyry, and Iamblichus for biographical details. Burkert (1972, p. 109) states that Aristoxenus and Dicaearchus are the most important accounts.
Aristotle had written a separate work On the Pythagoreans, which is no longer extant. However, the Protrepticus possibly contains parts of On the Pythagoreans. His disciples Dicaearchus, Aristoxenus, and Heraclides Ponticus had written on the same subject. These writers, late as they are, were among the best sources from whom Porphyry and Iamblichus drew, while still adding some legendary accounts and their own inventions to the mix. Hence, historians are often reduced to considering the statements based on their inherent probability, but even then, if all the credible stories concerning Pythagoras were supposed true, his range of activity would be impossibly vast.
Life
According to Clement of Alexandria, Pythagoras was a disciple of Soches, the Egyptian archprophet, and Plato of Sechnuphis of Heliopolis. Herodotus, Isocrates, and other early writers agree that Pythagoras was the son of Mnesarchus, born on a Greek island in the eastern Aegean called Samos. Pythagoras's father was a gem-engraver or a merchant from Tyre. Pythagoras's name led him to be associated with Pythian Apollo; Aristippus explained his name by saying, "He spoke (agor-) the truth no less than did the Pythian (Pyth-)", and Iamblichus tells the story that the Pythia prophesied that his pregnant mother would give birth to a man supremely beautiful, wise, and beneficial to humankind. A late source gives his mother's name as Pythais. As to the date of his birth, Aristoxenus stated that Pythagoras left Samos in the reign of Polycrates, at the age of 40, which would give a date of birth around 570 BC.
Pythagoras's later fate is unknown and inconsistent among ancient sources. Some say that he perished in the temple with his disciples, others that he fled first to Tarentum, and that, being driven from there, he escaped to Metapontum, and there according to Diogenes Laërtius, starved himself to death. His tomb was shown at Metapontum in the time of Cicero.
According to Walter Burkert (1972)
"Most obvious is the contradiction between Aristoxenus and Dicaearchus, regarding the catastrophe that overwhelmed the Pythagorean society. One of the two reports must be basically wrong: either Pythagoras withdrew to Metapontum before the outbreak of the unrest and died there (as Aristoxenus says) or he and his followers were hounded from city to city (as Dicaearchus has it). Like his doctrines, the life of Pythagoras also becomes a mirror image of real controversies in the schools. On the one hand there is the controversy over the primacy of the theoretical or practical life. In this respect Heraclides thinks Pythagoras as the apostle of pure 'theory'."
"There is not a single detail in the life of Pythagoras that stands uncontradicted. But it is possible, from a more or less critical selection of the data, to construct a plausible account."
According to Iamblichus (ca. 245–325 AD, 1918 translation) in The life of Pythagoras, translated by Thomas Taylor
"Twenty-two years Pythagoras remained in Egypt, pursuing closely his investigations, visiting every place famous for its teachings, every person celebrated for wisdom. Astronomy and geometry he especially studied and he was thoroughly initiated in all the mysteries of the gods, till, having been taken captive by the soldiers of Cambyses, he was carried to Babylon. Here the Magi instructed him in their venerable knowledge and he arrived at the summit of arithmetic, music and other disciplines. After twelve years he returned to Samos, being then about fifty-six years of age."
Family
According to some accounts, Pythagoras married Theano, a lady of Croton. Theano was also a philosopher, and said to have first been Pythagoras' pupil. According to Mary Ritter Beard, Theano told Hippodamus of Thurium (possibly Hippodamus of Miletus, who as per Aristotle planned the city of Thurium), that her treatise On Virtue contained the doctrine of the golden mean.
According to Thesleff, Stobaeus and Heeren, in On Piety, Theano wrote that:
I have learned that many of the Greeks believe Pythagoras said all things are generated from number. The very assertion poses a difficulty: How can things which do not exist even be conceived to generate? But he did not say that all things come to be from number; rather, in accordance with number - on the grounds that order in the primary sense is in number and it is by participation in order that a first and a second and the rest sequentially are assigned to things which are counted.
Their children are variously stated to have included a son, Telauges, and three daughters, Damo, Arignote, and Myia (who married to a famous wrestler, Milo of Croton). Milo was said to be an associate of Pythagoras. One story tells of the wrestler saving the philosopher's life when a roof was about to collapse.
Arignote wrote a Bacchica concerning the mysteries of Demeter, and a work called The Rites of Dionysus. Among the Pythagorean Sacred Discourses there is a dictum attributed to Arignote:
The eternal essence of number is the most providential cause of the whole heaven, earth and the region in between. Likewise it is the root of the continued existence of the gods and daimones, as well as that of divine men."
Brewer (1894) mentioned that "Pythagoras taught that the sun is a movable sphere in the centre of the universe, and that all the planets revolve round it." Thus, it would appear that Arignote's quote above is not entirely in alignment with his model of the universe, since it is limited to Earth orbit.
Influence
Before 520 BC, on one of his visits to Egypt or Greece, Pythagoras might have met the c. 54 years older Thales of Miletus. Thales was a philosopher, scientist, mathematician, and engineer, also known for the Thales' Theorem. Pythagoras' birthplace, the island of Samos, is situated in the Northeast Aegean Sea not far from Miletus.
In the absence of reliable information, however, a huge range of teachers were assigned to Pythagoras. Some made his training almost entirely Greek, others exclusively Egyptian and Oriental. We find mentioned as his instructors Creophylus, Hermodamas of Samos, Bias, Thales, Anaximander (a pupil of Thales), and Pherecydes of Syros.
In Lives and Opinions of Eminent Philosophers, Diogenes Laërtius (3rd century CE) cites the statement of Aristoxenus (4th century BCE) that the Delphic Themistoclea (also known as Aristoclea) taught Pythagoras his moral doctrines: "Aristoxenus says that Pythagoras got most of his moral doctrines from the Delphic priestess Themistoclea."
Porphyry (233 – 305 CE) calls her Aristoclea (Aristokleia), and wrote:"He (Pythagoras) taught much else, which he claimed to have learned from Aristoclea at Delphi."
The Egyptians are said to have taught him geometry, the Phoenicians arithmetic, the Chaldeans astronomy, the Magians the principles of religion and practical maxims for the conduct of life. Of the various claims regarding his Greek teachers, Pherecydes of Syros is mentioned most often.
According to R.D. Hicks (1972) Pythagoras not only visited Egypt and learnt the Egyptian language (Antiphon in the book On Men of Outstanding Merit), but also "journeyed among the Chaldaeans and Magi." Later in Crete, he went to the Cave of Ida with Epimenides; and entered Egyptian sanctuaries for the purpose to learn information concerning the secret lore of the different gods. Plutarch asserted in his book On Isis and Osiris that during his visit to Egypt, Pythagoras received instruction from the Egyptian priest Oenuphis of Heliopolis. Other ancient writers asserted his visit to Egypt. Enough of Egypt was known to attract the curiosity of an inquiring Greek, and contact between Samos and other parts of Greece with Egypt is mentioned.
Ancient authorities note the similarities between the religious and ascetic peculiarities of Pythagoras with the Orphic or Cretan mysteries, or the Delphic oracle.
Views
There is little direct evidence as to the kind and amount of knowledge which Pythagoras acquired, or as to his definite philosophical views. Everything of the kind mentioned by Plato and Aristotle is attributed not to Pythagoras, but to the Pythagoreans. Heraclitus stated that he was a man of extensive learning; and Xenophanes claimed that he believed in the transmigration of souls. Xenophanes mentions the story of his interceding on behalf of a dog that was being beaten, professing to recognise in its cries the voice of a departed friend. Pythagoras is supposed to have claimed that he had been Euphorbus, the son of Panthus, in the Trojan war, as well as various other characters, a tradesman, a courtesan, etc. In his book The Life of Apollonius of Tyana, Philostratus wrote that Pythagoras knew not only who he was himself, but also who he had been.
Many mathematical and scientific discoveries were attributed to Pythagoras, including his famous theorem, as well as discoveries in the field of music, astronomy, and medicine. It is mentioned that the people of Croton were supposed to have identified him with the Hyperborean Apollo, and he was said to have practised divination and prophecy. In the visits to various places in Greece – Delos, Sparta, Phlius, Crete, etc. which are ascribed to him, he usually appears either in his religious or priestly guise, or else as a lawgiver.
Excerpt from a speech by the character ‘Aristotle’ in Protrepticus (Hutchinson and Johnson, 2015)
"This is the thing for the sake of which nature and the god engendered us. So what is this thing? When Pythagoras was asked, he said, ‘to observe the heavens,’ and he used to claim that he himself was an observer of nature, and it was for the sake of this that he had passed over into life. And they say that when somebody asked Anaxagoras for what reason anyone might choose to come to be and be alive, he replied to the question by saying, ‘To observe the heavens and the stars in it, as well as moon and sun,’ since everything else at any rate is worth nothing." (p. 48)
Croton
After his travels, Pythagoras moved (around 530 BC) to Croton, in Italy (Magna Graecia). Possibly the tyranny of Polycrates in Samos made it difficult for him to achieve his schemes there. His later admirers claimed that Pythagoras was so overburdened with public duties in Samos, because of the high estimation in which he was held by his fellow-citizens, that he moved to Croton. On his arrival in Croton, he quickly attained extensive influence, and many people began to follow him. Later biographers tell fantastical stories of the effects of his eloquent speech in leading the people of Croton to abandon their luxurious and corrupt way of life and devote themselves to the purer system which he came to introduce.
According to Diogenes Laërtius, his followers established a select brotherhood or club (see below school) for the purpose of pursuing the religious and ascetic practices which developed. According to Diogenes Laërtius, what was done and taught among the members was kept a secret. The esoteric teachings may have concerned science and mathematics, or religious doctrines, and may have been connected with the worship of Apollo. Temperance of all kinds seems to have been strictly urged. There is disagreement among the biographers as to whether Pythagoras forbade all animal food, or only certain types. The club was in practice at once "a philosophical school, a religious brotherhood, and a political association".
Conflict seems to have broken out between the towns of Sybaris and Croton. The forces of Croton were headed by the Pythagorean Milo, and it is likely that the members of the brotherhood took a prominent part. After the decisive victory by Croton, a proposal for establishing a more democratic constitution, was unsuccessfully resisted by the Pythagoreans. Their enemies, headed by Cylon and Ninon, the former of whom is said to have been irritated by his exclusion from the brotherhood, roused the populace against them. An attack was made upon them while assembled either in the house of Milo, or in some other meeting-place. The building was set on fire, and many of the assembled members perished; only the younger and more active escaping. Similar commotions ensued in the other cities of Magna Graecia in which Pythagorean clubs had been formed.
As an active and organised brotherhood the Pythagorean order was everywhere suppressed, and did not again revive. Still the Pythagoreans continued to exist as a sect, the members of which kept up among themselves their religious observances and scientific pursuits, while individuals, as in the case of Archytas, acquired now and then great political influence.
Writings
No texts by Pythagoras are known to have survived, although forgeries under his name — a few of which remain extant — did circulate in antiquity. Critical ancient sources like Aristotle and Aristoxenus cast doubt on these writings. Ancient Pythagoreans usually quoted their master's doctrines with the phrase autos ephe ("he himself said") — emphasising the essentially oral nature of his teaching.
According to Sir William Smith (1870) (see book screenshot for full quote)
"It appears, in fact, from this, as well as from the extant fragments, that the first book of the work contained a general account of the origin and arrangement of the universe. The second book appears to have been an exposition of the nature of numbers, which in the Pythagorean theory are the essence and source of all things." (p. 305)
Mathematics
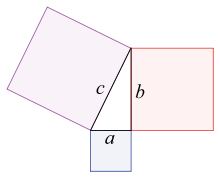
The Pythagorean theorem: The sum of the areas of the two squares on the legs (a and b) equals the area of the square on the hypotenuse (c).
Aristotle, Metaphysics 1–5 , cc. 350 BC
The so-called Pythagoreans, who were the first to take up mathematics, not only advanced this subject, but saturated with it, they fancied that the principles of mathematics were the principles of all things.
Since the fourth century AD, Pythagoras has commonly been given credit for discovering the Pythagorean theorem, a theorem in geometry that states that in a right-angled triangle the area of the square on the hypotenuse (the side opposite the right angle) is equal to the sum of the areas of the squares of the other two sides—that is, a 2 + b 2 = c 2 {\displaystyle a^{2}+b^{2}=c^{2}} .
While the theorem that now bears his name was known and previously utilised by the Babylonians and Indians, he, or his students, are often said to have constructed the first proof. It must, however, be stressed that the way in which the Babylonians handled Pythagorean numbers implies that they knew that the principle was generally applicable, and knew some kind of proof, which has not yet been found in the (still largely unpublished) cuneiform sources. Because of the secretive nature of his school and the custom of its students to attribute everything to their teacher, there is no evidence that Pythagoras himself worked on or proved this theorem. For that matter, there is no evidence that he worked on any mathematical or meta-mathematical problems. Some attribute it as a carefully constructed myth by followers of Plato over two centuries after the death of Pythagoras, mainly to bolster the case for Platonic meta-physics, which resonate well with the ideas they attributed to Pythagoras. This attribution has stuck down the centuries up to modern times. The earliest known mention of Pythagoras's name in connection with the theorem occurred five centuries after his death, in the writings of Cicero and Plutarch.
Musical theories and investigations
According to legend, the way Pythagoras discovered that musical notes could be translated into mathematical equations was when he passed blacksmiths at work one day and thought that the sounds emanating from their anvils were beautiful and harmonious and decided that whatever scientific law caused this to happen must be mathematical and could be applied to music. He went to the blacksmiths to learn how the sounds were produced by looking at their tools. He discovered that it was because the hammers were "simple ratios of each other, one was half the size of the first, another was 2/3 the size, and so on".
This legend has since proven to be false by virtue of the fact that these ratios are only relevant to string length (such as the string of a monochord), and not to hammer weight. However, it may be that Pythagoras was indeed responsible for discovering the properties of string length.
Pythagoreans elaborated on a theory of numbers, the exact meaning of which is still debated among scholars. Another belief attributed to Pythagoras was that of the "harmony of the spheres". Thus the planets and stars moved according to mathematical equations, which corresponded to musical notes and thus produced a symphony.
Brewer (1894), wrote (page 2614):
"The music or harmony of the spheres. Pythagoras, having ascertained that the pitch of notes depends on the rapidity of vibrations, and also that the planets move at different rates of motion, concluded that the sounds made by their motion must vary according to their different rates of motion. As all things in nature are harmoniously made, the different sounds must harmonise, and the combination he called the “harmony of the spheres.” Kepler has a treatise on the subject."
Tetractys
Pythagoras was also credited with devising the tetractys, the triangular figure of four rows which add up to the perfect number, ten. As a mystical symbol, it was very important to the worship of the Pythagoreans who would swear oaths by it.
Iamblichus, Vit. Pyth., 29
"And the inventions were so admirable, and so divinised by those who understood them, that the members used them as forms of oath: 'By him who handed to our generation the tetractys, source of the roots of ever-flowing nature.'"
Brewer (1894), wrote (page 2732):
"The four letters, meaning the four which compose the name of Deity. The ancient Jews never pronounced the word Jehovah composed of the four sacred letters JHVH. The word means 'I am,' or 'I exist' (Exod. iii. 14); but Rabbi Bechai says the letters include the three times— past, present, and future. Pythagoras called Deity a Tetrad or Tetractys, meaning the 'four sacred letters.'"
Religion and science
Heraclides Ponticus reports the story that Pythagoras claimed that he had lived four previous lives that he could remember in detail. One of his past lives, as reported by Aulus Gellius, was as a beautiful courtesan. According to Xenophanes, Pythagoras heard the cry of his dead friend in the bark of a dog.
Brewer (1894), wrote (page 2293):
"Pythagoras maintained that the soul has three vehicles: (1) the ethereal, which is luminous and celestial, in which the soul resides in a state of bliss in the stars; (2) the luminous, which suffers the punishment of sin after death; and (3) the terrestrial, which is the vehicle it occupies on this earth."
"Pythagoras asserted he could write on the moon. His plan of operation was to write on a looking—glass in blood, and place it opposite the moon, when the inscription would appear photographed or reflected on the moon's disc."
"Mesmerism was practised by Pythagoras, if we may credit Iamblichus, who tells us that he tamed a savage Daunian bear by “stroking it gently with his hand;” subdued an eagle by the same means; and held absolute dominion over beasts and birds by 'the power of his voice,' or 'influence of his touch.'"
"Pythagoras taught that the sun is a movable sphere in the centre of the universe, and that all the planets revolve round it. This is substantially the same as the Copernican and Newtonian systems."
"The Pythian games were held by the Greeks at Pytho, in Phocis, subsequently called Delphi. They took place every fourth year, the second of each Olympiad."
Lore
Pythagoras became the subject of elaborate legends surrounding his historic persona. Aristotle described Pythagoras as a wonder-worker and somewhat of a supernatural figure, attributing to him such aspects as a golden thigh, which he showed to Abaris, the Hyperborean priest, and exhibited in the Olympic games. According to Muslim tradition, Pythagoras was said to have been initiated by Hermes (Egyptian Thoth).
Brewer (1894), wrote (page 2292):
Pythagoras maintained that he distinctly recollected having occupied other human forms before his birth at Samos: (1) He was AEthalides, son of Mercury; (2) Euphorbos the Phrygian, son of Panthoos, in which form he ran Patroclos through with a lance, leaving Hector to dispatch the hateful friend of Achilles; (3) Hermotimos, the prophet of Clazomenae; and'(4) a fisherman. To prove his Phrygian existence he was taken to the temple of Hera, in Argos, and asked to point out the shield of the son of Panthoos, which he did without hesitation. (See Rat.)
Pythagoreanism
Both Plato and Isocrates affirm that, above all else, Pythagoras was famous for leaving behind him a way of life. According to Timaeus of Locri, he was the first to say, Friends have all things in common and Friendship is equality.
Brewer (1894), wrote (page 2685):
"In deadly hostility, ready to fight each other with swords. Poke not fire with a sword. This was a precept of Pythagoras, meaning add not fuel to fire, or do not irritate an angry man by sharp words which will only increase his rage." (See Iamblichus Protreptics, symbol ix.)
According to Walter Burkert (1972, p. 109)
"The history of Pythagoreanism was already, at that time, the laborious reconstruction of something lost and gone. It is only post-Aristolian sources that biographical and historical details regarding Pythagoras and the Pythagoreans are to be found."
Pythagorean school
According to Iamblichus (ca. 245–325 AD, 1918 translation) in The life of Pythagoras
"There were also two forms of philosophy, for the two genera of those that pursued it: the Acusmatici and the Mathematici. The latter are acknowledged to be Pythagoreans by the rest but the Mathematici do not admit that the Acusmatici derived their instructions from Pythagoras but from Hippasus. The philosophy of the Acusmatici consisted in auditions unaccompanied with demonstrations and a reasoning process; because it merely ordered a thing to be done in a certain way and that they should endeavour to preserve such other things as were said by him, as divine dogmas. Memory was the most valued faculty. All these auditions were of three kinds; some signifying what a thing is; others what it especially is, others what ought or ought not to be done." (p. 61)
"The best of all legislators came from the school of Pythagoras, Charondas, the Catanean, Zaleucus and Timaratus as well as many others, who established laws with great benevolence and political science." (p. 26)
"The whole Pythagoric school produced appropriate songs, which they called exartysis or adaptations; synarmoge or elegance of manners and apaphe or contact, usefully conducting the dispositions of the soul to passions contrary to those which it before possessed. By musical sounds alone unaccompanied with words they healed the passions of the soul and certain diseases, enchanting in reality, as they say. It is probable that from hence this name epode, i. e., "enchantment," came to be generally used.
For his disciples, Pythagoras used divinely contrived mixtures of diatonic, chromatic and enharmonic melodies, through which he easily transferred and circularly led the passions of the soul in a contrary direction, when they had recently and in an irrational and secret manner been formed; such as sorrow, rage and pity, absurd emulation and fear, all-various desires, angers and appetites, pride, supineness and vehemence. Each of these he corrected through the rule of virtue, attempering them through appropriate melodies, as well as through certain salubrious (health giving) medicine." (p.43)
Carl B. Boyer (1968), mentioned that "the Pythagorean school of thought was politically conservative and with a strict code of conduct." Leonid Zhmud (2006), identified two camps with the early Pythagoreans, the scientific mathematici and the religious acusmatici, who engaged in politics. According to Reidwig and Rendall (2005), who cite Antiphon reports, the school name was Semicircle, a place to discuss common interest topics among Samians. Outside of Samos he adapted a cave where he studied and lived day and night, discoursing with a few of his associates. In Samos he may have instructed the small athlete Eurymenes to eat a certain amount of meat every day.
Both Iamblichus and Porphyry give detailed accounts of the organisation of the school, although the primary interest of both writers is not historical accuracy, but rather to present Pythagoras as a divine figure, sent by the gods to benefit humankind.
Pythagoras set up an organisation which was in some ways a school, in some ways a brotherhood (and here it should be noted that sources indicate that as well as men there were many women among the adherents of Pythagoras), and in some ways a monastery. It was based upon the religious teachings of Pythagoras and was very secretive. The adherents were bound by a vow to Pythagoras and each other, for the purpose of pursuing the religious and ascetic observances, and of studying his religious and philosophical theories. There is mentioning of an oath on the Tetractys.
There were ascetic practices (many of which had, perhaps, a symbolic meaning). Some represent Pythagoras as forbidding all animal food, advocating a plant-based diet, and prohibiting consumption of beans. This may have been due to the doctrine of metempsychosis. Other authorities contradict the statement. According to Aristoxenus, he allowed the use of all kinds of animal food except the flesh of oxen used for ploughing, and rams. There is a similar discrepancy as to the prohibition of fish and beans. But temperance of all kinds seems to have been urged. It is also stated that they had common meals, resembling the Spartan system, at which they met in companies of ten.
Considerable importance seems to have been attached to music and gymnastics in the daily exercises of the disciples. Their whole discipline is represented as encouraging a lofty serenity and self-possession, of which, there were various anecdotes in antiquity. Iamblichus (apparently on the authority of Aristoxenus) gives a long description of the daily routine of the members, which suggests many similarities with Sparta. The members of the sect showed a devoted attachment to each other, to the exclusion of those who did not belong to their ranks. There were even stories of secret symbols, by which members of the sect could recognise each other, even if they had never met before.
Commentary from Sir William Smith, Dictionary of Greek and Roman Biography and Mythology (1870, p. 620).
At one point, the active and organised brotherhood the Pythagorean order was everywhere suppressed, and did not again revive, though it was probably a long time before it was put down in all the Italian cities [Lysis; Philolaus]. Still the Pythagoreans continued to exist as a sect, the members of which kept up among themselves their religious observances and scientific pursuits, while individuals, as in the case of Archytas, acquired now and then great political influence. Respecting the fate of Pythagoras himself, the accounts varied.
Influence
Influence on Plato
Pythagoras, or in a broader sense, the Pythagoreans, allegedly exercised an important influence on the work of Plato. According to R. M. Hare, this influence consists of three points: (1) The platonic Republic might be related to the idea of "a tightly organised community of like-minded thinkers", like the one established by Pythagoras in Croton. (2) There is evidence that Plato possibly took from Pythagoras the idea that mathematics and, generally speaking, abstract thinking is a secure basis for philosophical thinking as well as "for substantial theses in science and morals". (3) Plato and Pythagoras shared a "mystical approach to the soul and its place in the material world". It is probable that both were influenced by Orphism.
Aristotle claimed that the philosophy of Plato closely followed the teachings of the Pythagoreans, and Cicero repeats this claim: Platonem ferunt didicisse Pythagorea omnia ("They say Plato learned all things Pythagorean"). Bertrand Russell, in his A History of Western Philosophy, contended that the influence of Pythagoras on Plato and others was so great that he should be considered the most influential of all Western philosophers.
Politics and science
Pythagoras was the first person known to have taught the earth was spherical, with antipodes and that it revolved around the sun. Pythagoras was also said to have spread the seeds of political liberty to Crotona, Sybaris, Metapontum, Rhegium, Sicily, Tauromenium, Catana, Agrigentum and Himera.
Influence on Greek art
In the arts the Greeks searched some reality behind the appearances of things. The early Archaic sculpture represents life in simple forms, and it seems that it was influenced by the earliest Greek natural philosophies. There was a general Greek belief that nature expresses itself in ideal forms, and it was represented by a type (εἶδος), which was mathematically calculated. This can be observed in the construction of the first temples. The original forms were considered divine, and the forms of the later marble or stone elements indicate that there was an original wooden prototype. When the dimensions changed, the architects searched in mathematics some permanent principles behind the appearances of things. Maurice Bowra believes that these ideas influenced the theory of Pythagoras and his students who asserted that "all things are numbers".
During the 6th century BC, there was an evolution in the arts from the natural philosophies to the metaphysical theory of Pythagoras. The Greek sculptors and architects, tried to find the mathematical relation (canon), which would lead to the aesthetic perfection. The sculptor Polykleitos in his Canon wrote that beauty consists in the proportion not of the elements (materials), but of the parts, that is the interrelation of parts with one another and with the whole. It seems that he was influenced by the theories of Pythagoras. The numbers were extensively used in the Greek architectural orders. In the architectural canons every element was calculated and constructed by mathematical relations. The universe was controlled by the order, and even the sounds were functions of number and ratio. Rhys Carpenter says that he ratio 2:1 was the generative ratio of the Doric order, and in Hellenistic times an ordinary Doric colonnade, beats out a rhythm of notes."
Influence on other groups
Pythagoreanism may had an effect on Freemasonry and Rosicrucianism, both of which were groups dedicated to the study of mathematics/geometry and logical reasoning as opposed to religious dogma. Both Freemasonry and Rosicrucianism have claimed to have evolved out of the Pythagorean Brotherhood. Pythagorean mathematics are discussed in a chapter of Manly P. Hall's The Secret Teachings of All Ages entitled "Pythagorean Mathematics".
THE GOLDEN VERSES OF PYTHAGORAS12
While it is questionable as to whether anything Pythagoras wrote survived, the verses contained here do adequately capture the philosophy practiced by some of those that claimed to follow his teachings.
1. First worship the Immortal Gods, as they are established and ordained by the Law.
2. Reverence the Oath, and next the Heroes, full of goodness and light.
3. Honour likewise the Terrestrial Dæmons by rendering them the worship lawfully due to them.
4. Honour likewise thy parents, and those most nearly related to thee.
5. Of all the rest of mankind, make him thy friend who distinguishes himself by his virtue.
6. Always give ear to his mild exhortations, and take example from his virtuous and useful actions.
7. Avoid as much as possible hating thy friend for a slight fault.
8. [And understand that] power is a near neighbour to necessity.
9. Know that all these things are as I have told thee; and accustom thyself to overcome and vanquish these passions:--
10. First gluttony, sloth, sensuality, and anger.
11. Do nothing evil, neither in the presence of others, nor privately;
12. But above all things respect thyself.
13. In the next place, observe justice in thy actions and in thy words.
14. And accustom not thyself to behave thyself in any thing without rule, and without reason.
15. But always make this reflection, that it is ordained by destiny that all men shall die.
16. And that the goods of fortune are uncertain; and that as they may be acquired, so may they likewise be lost.
17. Concerning all the calamities that men suffer by divine fortune,
18. Support with patience thy lot, be it what it may, and never repine at it.
19. But endeavour what thou canst to remedy it.
20. And consider that fate does not send the greatest portion of these misfortunes to good men.
21. There are among men many sorts of reasonings, good and bad;
22. Admire them not too easily, nor reject them.
23. But if falsehoods be advanced, hear them with mildness, and arm thyself with patience.
24. Observe well, on every occasion, what I am going to tell thee:--
25. Let no man either by his words, or by his deeds, ever seduce thee.
26. Nor entice thee to say or to do what is not profitable for thyself.
27. Consult and deliberate before thou act, that thou mayest not commit foolish actions.
28. For it is the part of a miserable man to speak and to act without reflection.
29. But do that which will not afflict thee afterwards, nor oblige thee to repentance.
30. Never do anything which thou dost not understand.
31. But learn all thou ought'st to know, and by that means thou wilt lead a very pleasant life.
32. in no wise neglect the health of thy body;
33. But give it drink and meat in due measure, and also the exercise of which it has need.
34. Now by measure I mean what will not incommode thee.
35. Accustom thyself to a way of living that is neat and decent without luxury.
36. Avoid all things that will occasion envy.
37. And be not prodigal out of season, like one who knows not what is decent and honourable.
38. Neither be covetous nor niggardly; a due measure is excellent in these things.
39. Do only the things that cannot hurt thee, and deliberate before thou dost them.
40. Never suffer sleep to close thy eyelids, after thy going to bed,
41. Till thou hast examined by thy reason all thy actions of the day.
42. Wherein have I done amiss? What have I done? What have I omitted that I ought to have done?
43. If in this examination thou find that thou hast done amiss, reprimand thyself severely for it;
44. And if thou hast done any good, rejoice.
45. Practise thoroughly all these things; meditate on them well; thou oughtest to love them with all thy heart.
46. 'Tis they that will put thee in the way of divine virtue.
47. I swear it by him who has transmitted into our souls the Sacred Quaternion, the source of nature, whose cause is eternal.
48. But never begin to set thy hand to any work, till thou hast first prayed the gods to accomplish what thou art going to begin.
49. When thou hast made this habit familiar to thee,
50. Thou wilt know the constitution of the Immortal Gods and of men.
51. Even how far the different beings extend, and what contains and binds them together.
52. Thou shalt likewise know that according to Law, the nature of this universe is in all things alike,
53. So that thou shalt not hope what thou ought'st not to hope; and nothing in this world shall be hid from thee.
54. Thou wilt likewise know, that men draw upon themselves their own misfortunes voluntarily, and of their own free choice.
55. Unhappy that they are! They neither see nor understand that their good is near them.
56. Few know how to deliver themselves out of their misfortunes.
57. Such is the fate that blinds mankind, and takes away his senses.
58. Like huge cylinders they roll to and fro, and always oppressed with ills innumerable.
59. For fatal strife, innate, pursues them everywhere, tossing them up and down; nor do they perceive it.
60. Instead of provoking and stirring it up, they ought, by yielding, to avoid it.
61. Oh! Jupiter, our Father! if Thou would'st deliver men from all the evils that oppress them,
62. Show them of what dæmon they make use.
63. But take courage; the race of man is divine.
64. Sacred nature reveals to them the most hidden mysteries.
65. If she impart to thee her secrets, thou wilt easily perform all the things which I have ordained thee.
66. And by the healing of thy soul, thou wilt deliver it from all evils, from all afflictions.
67. But abstain thou from the meats, which we have forbidden in the purifications and in the deliverance of the soul;
68. Make a just distinction of them, and examine all things well.
69. Leaving thyself always to be guided and directed by the understanding that comes from above, and that ought to hold the reins.
70. And when, after having divested thyself of thy mortal body, thou arrivest at the most pure Æther,
71. Thou shalt be a God, immortal, incorruptible, and Death shall have no more dominion over thee.


