4.1: Notation
- Page ID
- 201630
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Rhythm can be a musician’s best friend or their worst nightmare. The symbols that we use in music to outline the rhythm of music are a different language format from melody and harmony but are used in tandem with the two to complete a full song. Rhythm also has its own system of rules so we have to learn a language within a language in order to write music at our fullest intellectual capacity.
In order to really understand rhythm, the theory student must have a separate practice time to focus on learning to count and identify rhythmic figures. To do that the student must understand the building blocks of rhythm that exist and how we apply them to composing music.
NOTATION
Composers and musicians have a standard set of rules that apply to counting and reading rhythm on the written page. There are several symbols that represent units of time that can be straightforward or manipulated in order to create an interesting sound or texture. Those units of time can mean to make a sound for a certain period of time or to not make a sound during a certain duration of time. The indication to not make a sound is referred to as a REST, meaning that the musician has no action to take but to keep track of the time as it unfolds to know when to re-enter the song and perform. For every duration of time, there is a symbol that means play or rest.
Below are the symbols that represent units of time that instruct the performer. It takes time to learn how to identify a particular note and how it is “drawn” on the staff in order to identify it on sight. Then try to connect to that symbol the “rest” symbol that denotes the same amount of time for fast recognition. Quickly analyzing a rhythmic passage allows the brain to focus on the other important factors of music performance. It is up to the student to memorize the symbols until they cannot be forgotten and then apply that knowledge by practice. Practice comes from getting as much sheet music as one can and counting every single rhythm all the way through. There are several method books for instruments or other theory books one can obtain with hundreds of musical examples to count and challenge the brain. Doing this on a regular basis as part of your practice regimen is the only way to get comfortable with this unique application of alphabet, fractions, and arithmetic.
The examples that follow list the rhythms one comes face to face within reading music. Using a single-lined staff, we can focus solely on the rhythm which allows us to absorb information quicker. We start with the largest note value.
Whole Note

The whole note, shown on the left, is a plain circle, which we can place on any space or line on the staff and the performer must play for four counts. If the performer has the symbol on the right side of the example they must remain silent for four counts.
Half Note

By cutting the whole note in half we get a note that lasts for two counts. This note is a circle with a line connected to it. Musicians refer to this line as a stem. The stem is important as it holds the key to identifying other rhythms as we keep cutting the values in half. The symbol on the right side of this example means the performer remains silent for two counts.
If one were to compare the half rest and whole rest they would see the whole rest is always hanging below a line and the half rest is on top of a line.
Quarter Note

Next, we cut the Half Note into two equal parts and the product is the quarter note. This note is represented by a filled-in circle with a stem and is one beat or count in duration. The “squiggly” symbol directly next to the note in the example is the quarter rest. The rest is the same time duration as one beat. Notice the half rest all the way on the right in the above example – one-quarter note plus one-quarter rest still leaves us with two counts in the 4/4 time signature we need to know what to do with; silence for those last two counts is indicated by the half rest.
Eighth Note

By cutting the quarter into two, we get the eighth note. This note is represented by a filled-in circle with a stem, but the stem has a small mark at the top musicians call a flag. The more flags on the note the shorter the duration. This is one of the most important notes to understand because it is the underlying rhythmic framework of all of music. This note’s duration is for half of a count. In fact, the shorter time durations become a tool musicians use to communicate to each other the feel of a song. They refer to this as SUBDIVIDING the BEAT, which means feeling the space in between the unit of measurement to ensure the groove of a song can be felt by the listener and other performers. The symbol directly to the right of the eighth note – a slash with a reverse flag – is the corresponding rest that has the same duration (an eighth rest).
Sixteenth Note

By chopping the eighth note in half we get the sixteenth note, an even shorter duration of time. This note moves quickly, even in slower tempos. It is represented by a filled in circle with a stem that has two flags. The corresponding rest is the same duration and has two reverse flags as its stem counterpart.
COUNTING RHYTHM
Now that we have identified the symbols used to communicate durations of time called rhythms, we must learn how to group them and communicate that grouping in a way that allows other performers and listeners to make musical sense of what they hear. We achieve this by using a system of numbers and letters to group rhythms into units of time that can be felt or graphically communicated on a staff.
This example demonstrates how we use numbers to identify beats within a measure of music. Once we reach a new measure we begin over 1, 2, 3, 4 and so forth. We do so because the quarter note is the unit of beat. We use numbers to denote units of beat.

In the event the composer wants the shorter duration of the eighth note then we use the numbers to identify the beats, but we use the + symbol to identify the notes between the numbers. Musicians refer to this symbol using the word “and”.

When we see the sixteenth note used in graphic notation we use the numbers to identify the beats, we keep the + to identify the eighth notes. We must also identify the notes between the eighths. To do this, musicians use the letter “e” right after the number and the letter “a” at the very end of the beat, pronounced “ah.” Counting the sixteenth notes aloud would sound like “one ee and ah, two ee and ah,” and so on.

Sometimes composers like to group the rhythm for a song in threes instead of the 2 by 2 system previously described. We call these TRIPLETS because they are grouped in threes, and we have a slightly different counting system for these. The number is still present to identify the beat, however, the syllables have changed. Musicians use “la” for the second note of a triplet and “li” for the past note of the beat. The example below shows eighth note triplets.
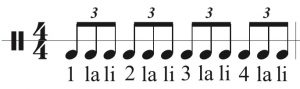
It is possible to cut these notes into halves as we did in previous examples and we need a different language to help identify each separate note of the beat. Sixteenth note triplets are called Sextuplets because they come in groups of six. We retain the number to identify the beat or count and we keep “la” and “li” but add “ta” to each note between la and li.

Counting odd and compound meters can be daunting at first, especially if the tempo is fast. However, the same rules and principles explained above apply to different numeric systems. The following example outlines a rhythmic passage written in 5-8 meter. An odd grouping and a smaller note value as the unit of beat. We still use numbers to identify the individual beats. However, because of the odd grouping, the 5-8 meter can be grouped in two different manners, which musicians refer to as a 2-3 grouping or a 3-2 grouping.

Especially difficult for beginning theory students is the 6/8 time signature. It is very straightforward in explanation, however, application during performance can cause frustration. We still use the numbers to identify the individual beats within a measure. The problem tends to occur with the grouping of the rhythm. The two groupings of three can be felt musically as two big units and mislead the listener or theory student if they are unaware. Performing within large bodies of instruments like a band or orchestra, everyone must subdivide the beat to know how their particular part fits within the entire group. The feeling of two large beats against the actual unit of 6 individual beats can be difficult to feel and perform.

Other odd meters like 7/8 can also be grouped in two ways. In 7-8 we can group them by a 3-4 grouping or a 4-3 grouping. Either way the number is still identifying the individual beat within the measure.

Compound meters such as the one shown below in 9/8 are also problematic. We can group these in units of three for efficiency but the individual beats are still numbered. The problem here is the even grouping of three; if they are not aware, the listener or theory student can feel the big units of 3 as the beat when in fact it is the smaller units. The same can be said about the 12/8 example.
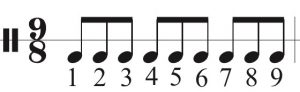

When it comes to subdividing compound meters we follow the same formula as before in which the numbers identify specific beats within a measure and the symbol for “and” (+) is used to mark the subdivision as seen in the example below.

By studying the building blocks of creating rhythms and how they work as a unit to define a musical selection, we can gain a deeper understanding of music as a whole. This is achieved through the study of “The Whole Note Break Down.” The following graphic demonstrates how the rhythmic symbols are related and how they define the rhythmic rules one must use to create or read rhythm. Beginning with the Whole Note, each symbol represents a unit of time. Those durations have a mathematical relationship with each other that allows multiple rhythms to exist within a single time frame.
THE WHOLE NOTE BREAKDOWN

METER AND TIME SIGNATURES
The previous graph shows the symbols we use to denote amounts of time (durations) we desire a specific note to be performed. One of the most important tools in reading music is understanding how time signatures work. We get our numeric representation from the math that exists from slicing everything in half until we have very small chunks of time starting with the Whole Note. It has 4 counts that we divide to get ½ (one half), divide this to get ¼ (one quarter), divide this to get ⅛ (one eighth), and divide this to get 1/16 (one-sixteenth). We then use these groupings based on simple fractional math to define large areas of music.
The most common meter used in popular music production is referred to as COMMON TIME or 4/4. This meter is easy to feel for non-musicians and is evenly divisible so that the rhythmic structure is memorable. We call it common because of its virtual dominance of all music creation.
Common Time

We use the Whole Note Breakdown chart to give meaning to the bottom number. Because there is a 4 on the bottom of the time signature, the Quarter Note is the unit of beat. If an 8 resides there then the Eighth Note is the unit of beat per measure. We can mix and match our meters based on simple mathematical formulas to create complex and diverse groove patterns that help to define the composition in a more efficient, clear format.
We divide METER into two different categories, SIMPLE METER and COMPOUND METER. Simple meter is even and divisible by even units, usually 2’s and 4’s. Compound meter is grouped into odd number groupings such as 5, 6, or 7.
Simple Meters:

Compound Meters:

When composers need to alter the time scale to fit musical needs, they often take simple and compound meters and mix them together in some type of pattern that is a smaller unit of the form or a smaller part of the whole that makes the entire composition. Mixed meters can be very tricky when one is just learning to count and feel time. Go slowly because sometimes even though the math is simple, it won’t work out the way you think.
MIXED METER

The previous example demonstrates compound meter composition that moves between even and odd meters creating a specific type of groove and feel. There are two ways composers can alter rhythm by applying different forms of math to the rhythmic modulation:
- The original unit of beat remains constant all the way through so that the rhythmic groupings become flexible in relation to where it began.
- We change the unit of beat with each meter change meaning that the original feel will be altered by speeding or slowing of rhythmic time.
In compositions with metric modulation or rhythmic modulation, the composer will denote their intentions in the music at the moment the meter changes. They can choose to keep the original unit of meter in place and the meter changes will yield a specific groove or rhythmic product that sounds more relatable to the overall composition. If, on the other hand, they desire a more dramatic change in the rhythmic aspect of the song they can choose to change the unit with each rhythmic modulation. This is particularly difficult to perform and you may not experience this unless you attend a music school and become a music major. Music majors must practice constantly and play many songs that challenge their rhythmic skill set in order to be able to call themselves professional musicians.
It is of great importance that the new theory student obtains a metronome. It will help keep consistent time in order to practice rhythm alone without harmony or melody. Any student can do this by using pre-existing sheet music or method books, especially percussion method books. Many percussion method books are devoted solely to rhythmic understanding because so much of a percussionists’ job is providing the feel and groove of a song for the rest of the group to play over.

