2.3: Modes
- Page ID
- 168980
The first mode to study is referred to as the IONIAN mode and is constructed with the same formula of half steps and whole steps as a major scale.

The next mode is referred to as the DORIAN mode and it is constructed the same as a natural minor scale. However, in this scale, the 6th scale degree is raised one half-step.

The third mode is referred to as the PHRYGIAN mode and is constructed as a natural minor scale with a lowered 2nd scale degree.

The fourth mode is referred to as the LYDIAN mode and is constructed as a major scale with a raised 4th scale degree.

The fifth mode is referred to as the MIXOLYDIAN mode and is constructed as a major scale with a lowered 7nth scale degree.
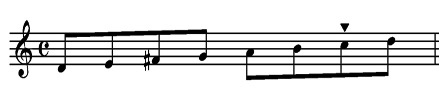
The sixth mode is referred to as the AEOLIAN mode and is constructed as a natural minor scale.

The seventh mode is referred to as the LOCRIAN mode. This mode is difficult to discuss because there is no analogy to make in order to compare it to what we use regularly in improvisation. So we use the half-step/whole-step formula H-W-W-H-W-W-W to represent the Locrian mode.
HOW WE USE SCALES
At the beginning of Western music development, melody provided the main vehicle for identifying a song. Eventually, music theorists and composers would break melodies down into smaller parts in order to identify different parts of a musical composition. Composers also began to identify different parts of melodies as phrases, which are constructed in the same manner a grammatically tight sentence is put together. The first and most basic way to analyze a melody is through ANTECEDENT and CONSEQUENT breakdowns of melodies that are composed by recognized masters of composition like J.S. Bach, Haydn, Mozart, and Beethoven. Jazz, Blues, and Pop musicians refer to this technique as QUESTION AND Answer or CALL AND RESPONSE.
The following example outlines the Call and Response technique

In other words, there is a phrase or melody constructed with an even measure structure, usually four or six measures (although we will use two for simplicity). Another melody that is the same length and key follows the first melody in order to form one larger unit, thus displaying balance and unity within the work.
Over time, composers became so masterful at creating and using melody that they began to give it another job besides song identification. Some composers use melody to represent characters of a story when that character’s presence is required for good storytelling. For example, in the first three Star Wars films by George Lucas(4,5,6), the composer John Williams is brilliant with melodic development which gives those pictures the ability to draw the audience into the story and hold their attention without them even realizing it. Every character has their own melody or theme that represents them. The audience hears these themes every time the characters are on screen. Williams even composed melodies that represented the relationships between different characters. It is practically impossible for anyone familiar with American Pop culture to hear the “Imperial March” and not picture Darth Vader coming down the hall.
Good composers use scales to draw on for musical substance. In order to create new material connected to the original idea, composers find a relationship within the construction of a melody to exploit in multiple ways. How they use those existing relationships will yield other artistic substance that ultimately relates to all parts of the piece in very subtle manners because it is all based on the original idea. Using and manipulating mathematical and musical relationships to divide and distribute melody is called a VARIATION. In order to be a good composer, one must be able to manipulate melodic development in a number of ways to create multiple VARIATIONS for musical interest.
Start out small. Write short effective melodies and try to find various ways to manipulate them. The best place to hear this technique in use is in Beethoven’s 5th Symphony. The entire composition is based on two notes used in a simple, repetitive manner that fuels the rhythm and harmonic content. Listen to the piece and how Beethoven masterfully flings around the main musical idea throughout the work in various instruments and various ranges, various dynamics, as solos and unison licks, and even the entire orchestra playing the theme together. Even in later movements, he is able to find new and unique ways to bend or flip the theme so that it sounds like the original statement while simultaneously giving the listener something new to digest.
The next graphic shows the first composition lesson everyone receives at the beginning of their creative journey. The ability to take only two notes and turn them into something musical is an important part of learning how to effectively compose good, balanced melodies.
Starting with a simple two-note main theme, use notes A and B that are one whole step in distance from each other to generate compositional material. We use two notes to start in order to isolate and learn each separate technique for music construction. With experience, a seasoned composer can use the rules outlined below with entire scales and original melodies or even create their own system of rules to follow. A good composer will sketch out ideas on how to expand the melody through variation. We extend the original statement by starting on the note B and going in reverse according to intervallic structure or creating a mirror image of the main theme, this is called RETROGRADE. A composer can create even more substance by inverting the original theme based on an intervallic relationship, called INVERSION. Finally, we can invert that new retrograde cell thus creating another part of the melodic whole.

Once a solid melody is constructed, the composer can elicit new melodic cells by using simple math and intervallic measurement to transpose their work up or down then transposing that melodic cell and so on, yielding a seemingly infinite amount of musical material. Creating multiple versions of a melody will also give clues as to which harmony structure to pick or whether to create your own. The spaces between the notes of a melody can also define the rhythmic values a composer uses to spell out a melody or when it arrives in the storytelling process.

