4.8: Creating a Search Statement
- Page ID
- 241966
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Combining Your Keywords
Once you have dissected your research question, found the main concepts, and listed several keywords to describe these concepts (e.g., synonyms, narrower terms, broader terms), it is time to combine those keywords in meaningful ways in order to perform a search for information resources. The combination of terms using various search strategies, called a search statement, will help you get more precise results than typing in a whole research question or just a few words into a search bar. Search statements are almost like a set of instructions given to whatever search option you are using (e.g., library catalog, library database) that describe what you want to find.
Boolean Operators
Named after the mathematician, George Boole, Boolean operators are used as conjunctions that combine or exclude certain keywords in your search. Though Boolean operators are used in logic, mathematics, and computer science, there are three common Boolean operators used by search engines (e.g., library catalogs, academic databases, and some online search engines). Think of Boolean operators as instructions that tell a search engine what to do with your keywords. Some search tools need Boolean operators to be typed in all capital letters in order for them to work, so it is a good idea to always type them in all caps whenever you are using them.
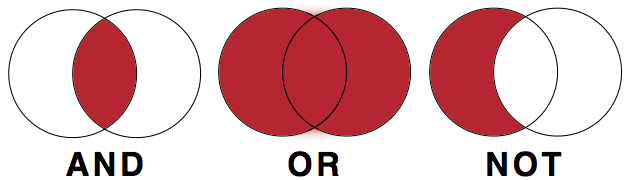
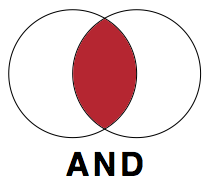
AND
The Boolean operator AND is used between all the keywords and phrases that you want to include in your search. When creating a search statement to find information on the effects of divorce on high school students’ GPA, the Boolean AND operator would go between our three keywords/phrases:
Divorce AND grade point average AND high school
By doing this, the information sources that will be returned in the results will all contain all three of these keywords/phrases somewhere within them.
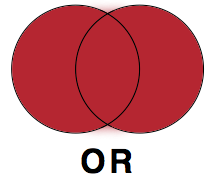
OR
The Boolean operator OR is used to search for alternative keywords. Remember, there are many words that one could use to describe the same concept and OR gives you the option to search for multiple, synonymous terms at once. Instead of searching for various alternative keywords in different searches, OR allows you to search for multiple alternative keywords in the same search.
grade point average OR academic achievement
NOT
The Boolean NOT excludes certain keywords from your search. This Boolean operator is not a commonly used one, but can be very helpful if you are getting many irrelevant results. Boolean NOT is best used when using keywords that have associations with multiple things. For instance, if you were trying to search for information on the animal Jaguar and kept getting too many results about the car brand Jaguar, you could use the NOT operator to exclude the word “car” from your search. Jaguar NOT car would exclude any information sources that contained the word car. Be aware that using NOT can exclude relevant results, as well. If an article or website that had some great information on the animal Jaguar, but just so happened to mention the word “car” in the text somewhere, it would be excluded from your results.
Washington NOT George
(when trying to find information on Washington the state, not George Washington)
Mexico NOT city
(when trying to find information on the entire country of Mexico not Mexico City)
Apple NOT fruit
(when trying to find information on Apple the computer company and not apples the fruit)

Phrase Searching
Phrase searching allows you to narrow down your search by specifying the exact order you want certain keywords to appear. Quotation marks around two or more keywords (also known as a “phrase”) will keep those words in that exact order during your search. For example, searching for the two keywords computer monitor without the quotation marks may find information sources that have nothing to do with computer monitors, but still contain the two words “computer” and “monitor” (e.g., an article about monitoring computer usage). Searching for “computer monitor” instead locks those keywords together as a unit and will only return results with that phrase “computer monitor.” Unless you are searching for a single keyword on its own, it’s a good idea to use phrase searching to make sure you are getting the most relevant results.
“Grade point average” OR “academic achievement”
Nesting
Just like Boolean, nesting is another concept taken from mathematics that is useful during information searches. When you are using more than one type of Boolean operator in your search statement, nesting—using parentheses around portions of your search statement—will help to organize what Boolean operators go with what keywords. Without nesting, most search engines and library databases will read your search statement from left to right, applying the Boolean operators in that sequence.
Let’s look at two examples:
Divorce AND (“grade point average” OR “academic achievement”) AND “high school”
Divorce AND “grade point average” OR “academic achievement” AND “high school”
In the first example, the search will yield results that contain either key phrase “grade point average” or “academic achievement,” but in the second example without the parentheses, the search will either look for information sources with both the keyword “divorce” and the key phrase “grade point average” or it will find information sources with the key word “high school” and the key phase “academic achievement.” The use of parentheses in this search statement would ensure that the Boolean OR is applied to the two alternative keywords.
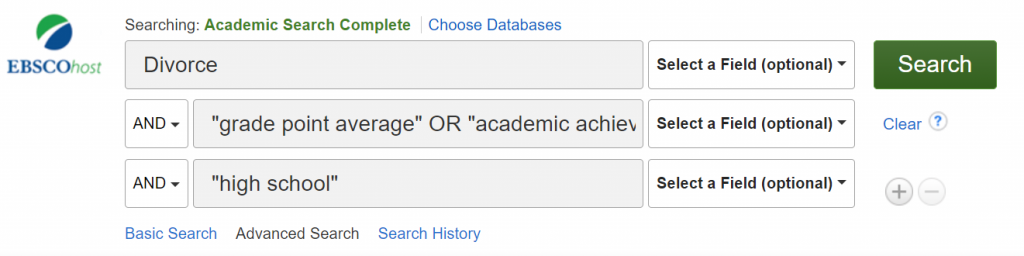
Library databases will have the option of either a basic or advanced search. A basic search will require that you type out Boolean operators (in all capital letters) and the parentheses used for nesting. The advanced search will offer you drop-down menus for Boolean operators. If your search statement requires nesting, type the portion of the search statement that would have gone in parenthesis all on one line. See the screenshots below to view the differences between a basic and advanced search.

Truncation
There may be times that you want to include all the different word forms of a certain keyword in your search without having to use the Boolean OR and type in each of the different word forms. To use truncation, type in the root word followed by a symbol. In most cases the symbol used for truncating words is the asterisk (*), but this may vary depending on the search engine or library database you are using. For example, searching for child* would return results containing the words child, children, childhood, childish, etc. Watch the following video [3:34] for an explanation of truncation, as well as phrase searching and nesting:
Note: Turn on closed captions with the “CC” button or use the text transcript(opens in new window) if you prefer to read.
Sources
“How Library Stuff Works: Boolean Modifiers “”, *, ( )”(opens in new window) by McMaster Libraries(opens in new window) is licensed under CC BY 4.0(opens in new window)
Images from “Search Statements(opens in new window)” by Teaching & Learning, Ohio State University Libraries,(opens in new window) licensed under CC BY 4.0(opens in new window)


