11.3.4: The Logic of If-Then
- Page ID
- 36227
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
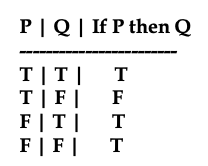
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In this section we explore the logic of conditionals. Some argument patterns involving conditionals are so common that they have been given names. The most common of all is modus ponens:
The validity of this form can be checked by using the truth table for implication (that is, the conditional) and noticing that there is no possibility of a counterexample, namely a situation where all the premises are true and the conclusion is false.
The Greek logician Chrysippus discovered the modus ponens form in 200 B.C.E. Here is an example of an argument whose sentential logical form is modus ponen s:
If they bought that much aluminum stock right before Chile had its general strike, then they will be wiped out.
They did buy that much aluminum stock just before Chile had its general strike.
They will be wiped out.
To show that this argument does have the modus ponens logical form, we could use this dictionary of abbreviations:
P = They bought that much aluminum stock right before Chile had its general strike.
Q = They will be wiped out.
If we symbolize the argument, then we get this logical form:
Choosing the letters P and Q was arbitrary. We could have used A and B. The following form is also called modus ponens:
If A then B
A
So, B
In addition to modus ponens, there are other forms of deductively valid reasoning in sentential logic. Modus tollens is another common one, and it has this form:
Examples of this form of valid reasoning were examined in earlier chapters without mentioning the Latin term for it. Here is an example:
If he is a lawyer, then he knows what the word tort means. Surprisingly, he doesn't know what the word means. So, he's not a lawyer.
In this example of modus tollens, the letters A and B represent the following:
A = He is a lawyer.
B = He knows what the word tort means.
In daily life, you wouldn't be apt to detect the modus tollens form so clearly because the above argument might be embedded in a passage like this:
If he were really a lawyer as he claims, he'd know the word tort. So, he's some sort of imposter.
This passage contains the same modus tollens argument that was in the previous passage. However, the premise not-B is now implicit. The conclusion of the modus tollens is also implicit. In addition, a second conclusion has been drawn—namely, that he's an imposter. It takes a lot more logical detective work to uncover the modus tollens argument.
Although the modus tollens form is a valid form—that is, any argument with that form is a valid argument—there are apparently similar arguments that are invalid yet are often mistaken for valid ones. Here is an example of a common one:
If she's Brazilian, then she speaks Portuguese. She's no Brazilian, so she doesn't speak the language.
The reasoning is deductively invalid. For purposes of symbolic logic, we will treat "She's no Brazilian" as the same sentence as "She is not Brazilian." In standard form, the argument can be written this way:
If she's Brazilian, then she speaks Portuguese.
She is not Brazilian.
-------------------------------------------------------------
She does not speak Portuguese.
The conclusion does not follow with certainty. To suppose it does is to commit the fallacy of denying the antecedent. The fallacy also occurs more transparently in this argument: "If you are a Nazi, then you breathe air, but you obviously are not a Nazi, so you don't breathe air." This invalid argument is logically analogous to the one about speaking Portuguese.
In sentential logic, the logical form of the fallacy is
The form is what defines the fallacy. The if-part of a conditional, the P, is called its antecedent. Then then-part is called the consequent. The second premise, "not-P," denies (negates) the antecedent. The arguer asserts the conditional, denies the antecedent, and draws an invalid inference. That is why the fallacy has the name it does.
Is the following argument valid?
Let us say that AI+ is artificial intelligence that is somewhat greater than human level. That is, AI+ is a little more intelligent than the most intelligent human. There will be AI+. Maybe in a decade or two. Let us say that AI++ (or super-intelligence) is AI of far greater than human level (say, at least as far beyond the most intelligent human as the most intelligent human is beyond a mouse). It is inevitable if AI+ occurs.
- Answer
-
Yes, it is valid. Here is the argument in standard form:
1. There will be AI+.
2. If there is AI+, there will be AI++.
───────────────────────
3. There will be AI++.”
Here is an invalid argument that is often mistaken for a modus ponens argument.
If she's Brazilian, then she speaks Portuguese. She does speak Portuguese. So she is Brazilian.
The premises of this argument do give a weak reason to believe the woman is Brazilian. However, if the arguer believes that the premises establish with certainty that she is Brazilian, then the arguer is committing the fallacy of affirming the consequent. Rewriting the argument in standard form yields
If she's Brazilian, then she speaks Portuguese.
She does speak Portuguese.
-----------------------------------------------------------
She is Brazilian.
The logical form, in sentential logic, of the fallacy is
The fallacy of affirming the consequent has its name because the then part of any conditional is called its consequent and because affirming the second premise Q affirms the consequent of the conditional.
Which one passage commits the fallacy of denying the antecedent?
a. If pork prices continued to drop in Japan from 1789 to 1889, then pork would have been eaten regularly by the average citizen of Tokyo in 1890. Pork prices continued to drop in Japan during that time. Consequently, the average citizen of Tokyo in 1890 did eat pork regularly.
b. If pork prices continued to drop in Japan from 1789 to 1889, then pork would have been eaten regularly by the average citizen of Tokyo in 1890. The average citizen of Tokyo in 1890 did not eat pork regularly. So, pork prices did not continue to drop in Japan from 1789 to 1889.
c. If pork prices continued to drop in Japan from 1789 to 1889, then pork would have been eaten regularly by the average citizen of Tokyo in 1890. So the average citizen of Tokyo in 1890 did not eat pork regularly, because pork prices did not continue to drop in Japan from 1789 to 1889.
d. If pork prices continued to drop in Japan from 1789 to 1889, then pork would have been eaten regularly by the average citizen of Tokyo in 1890. The average citizen of Tokyo in 1890 did not eat pork regularly. So, pork prices did continue to drop in Japan from 1789 to 1889.
e. If pork prices continued to drop in Japan from 1789 to 1889, then pork would have been eaten regularly by the average citizen of Tokyo in 1890. The average citizen of Tokyo in 1890 did eat pork regularly. So, pork prices did continue to drop in Japan from 1789 to 1889.
- Answer
-
Answer (c).
In the previous Concept Check, which passage commits the fallacy of affirming the consequent?
- Answer
-
Answer (e).
In the previous Concept Check, which passage is an example of modus ponens?
- Answer
-
Answer (a).
Logicians working in sentential logic have discovered many other deductively valid and invalid argument forms. For example:
In other words, the following argument form is deductively valid:
If someone says to you, "If it snows today, you should seek shelter at David's cabin," is the person implying that it is snowing today? No, and the point behind why the person is not is captured by the following invalid argument form:
The following inference is also deductively invalid:
You'd be surprised how many people make those two errors.
The techniques of sentential logic can often be helpful in analyzing deductive argumentation, but there are many deductive arguments for which sentential methods do not apply. The recognition of this fact has led logicians to create new and more powerful logics to handle these other arguments. These logics are studied in college courses called “symbolic logic” and “deductive logic” and “formal logic.”
Spotting the logical form of a sentence is a subtle skill; you cannot do it automatically. If you are not careful, then you will mistakenly think these two if-then sentences are equivalent, but they are not:
If Oswald didn't shoot President Kennedy, then someone else did.
If Oswald hadn't shot President Kennedy, then someone else would have.
The subtle difference in these two sentences is that our background knowledge tells us, perhaps implicitly, to evaluate the first sentence from the perspective of our present, but to evaluate the second from just before the President was shot.
Sometimes we logicians need to pay attention to the subjunctive mood, and sometimes we do not need to. For example, the following two sentences are equivalent and can be translated into symbolic logic with the same symbol, even though the second is in the subjunctive mood and the first is in the indicative mood:
If I shoot you, then you will die.
If I were to shoot you, then you would die.
Identify the logical form of the following reasoning about conditionals, and indicate whether it is or isn’t valid reasoning:
John: Are you sure?
Winona: If I wasn’t, I wouldn’t be here.
- Answer
-
This is valid reasoning. Let P be the implicit assumption that I am here. Let Q be the claim that I am sure. Then the reasoning has this valid logical form:
P
If Not Q,
then Not P
------------------------
Q


