27.2: Picturing Logical Structure
- Page ID
- 95281
Just as a good blueprint can help us visualize the spatial layout or structure of a house, a good diagram can help us grasp the logical layout or structure of a sentence or an argument. Indeed (as we will see below), in some cases when we draw the picture of the premises of an argument, the conclusion is automatically drawn in the process.
Consider the two very simple arguments below:
P1. All humans are mortal.
P2. Wilbur is human.
So, Wilbur is mortal.
P1. All even numbers are divisible by 2.
P2. 18 is an even number.
So, 18 is divisible by 2.
The two arguments have very different content or subject matter (human mortality vs. numbers), but they also have something very important in common. Both are valid, and they are valid for the same reason. As always, validity is based on form or structure, rather than content or subject matter, and these two arguments have the same logical structure. We can represent this common structure by erasing the content and just leaving the logical skeleton behind:
P1. All ____are____ .
P2. x is a _____.
So, x is a _____.
No matter how we plug content into these blanks, if we plug the same word or phrase into the same placeholder each time it occurs, and the result is a grammatical sentence, the resulting argument will be valid.
In the best case, you can draw a picture of the premises and you will find that your picture, without any further additions, also includes a picture of the conclusion. This is the case in some of the simpler examples of deductively valid arguments. Indeed, in these cases, teachers often draw a picture to convince their students that a given argument format is valid.
It will help if we imagine constructing a picture of this argument structure step by step (see Figure 27.2.1). We begin by drawing the first premise, putting a smaller circle representing humans entirely inside a larger circle representing creatures that are mortal (in the subfigure at the left).
Next, we draw the second premise by placing a letter representing Wilbur in the second circle (in the middle subfigure).
Finally, we need to draw the conclusion. But we find that in drawing the two premises, we already drew the conclusion. This occurred because the argument is valid, and as we saw earlier, the information in the conclusion is already contained in the premises. Since the information in the conclusion is already in the premises, our representation of the premises will automatically contain a representation of the conclusion.
The left and center diagrams in Figure 27.2.1 are already abstract, but in the diagram on the far right we remove the very last bit of content. This leaves just a picture of the argument’s form. It is now easy to see that—and why— any argument with this form must be valid. Some sentences and arguments do not lend themselves to a graphical representation, but many do, and for those that do, pictures can be very helpful. Of course, this is an easy example, and we don’t really need a diagram to understand it. But pictures really come into their own when we turn to more difficult or complex problems that can be hard to grasp without pictures (we will see an example below with the card-selection problem).
.png?revision=1&size=bestfit&width=775&height=240)
Conditionals and Conditional Arguments
Necessary and Sufficient Conditions
Thinking in terms of frequencies or proportions not only helps us get clearer about probabilities. It can also sometimes help us reason about conditionals. Take the conditional:
- If Fido is a dog, then he’s a mammal.
This sentence is about a specific dog, Fido, rather than about groups of any sort. But many (not all) conditionals like this are true (or false) because of facts about groups. Here, the fact that all dogs are mammals.
.png?revision=1&size=bestfit&width=245&height=230)
We can represent this statement with a diagram like that in Figure 27.2.2, and then we can use it to help us in our reasoning. We can place the dot representing Fido in the dog circle, and it’s immediately clear that he’s in the mammal circle.
So far, things are obvious. Our diagram also shows us why various, more complicated sentences are true or false. For example, if we place Fido’s dot anywhere outside the mammal circle, say out at location Z, there is no way he could be in the dog circle. So, the conditional:
If Fido is not a mammal, then he’s not a dog.
is also true.
Now let’s return to Figure 27.2.2 to see how necessary and sufficient conditions work.
- If something is inside the smaller, dog, circle, then it must be inside the larger, mammal, circle. Being in the smaller circle is sufficient – all that it takes – for being inside the outer circle. Since X is a dog, X is a mammal.
- If something is outside the outer circle, there is no way it could be inside the inner circle. As Y shows, being in the larger circle isn’t sufficient for being in the smaller one, but it is necessary.
In those cases where we can think of conditionals in terms of sets of things, the set (e.g., dogs) mentioned in the antecedent is the inner circle and the set (e.g., mammals) mentioned in the consequent is the outer circle. This makes it clear pictorially why antecedents are sufficient conditions and consequents are necessary conditions.
This is possible in many instances where it may be less obvious. Consider:
- If my alarm breaks tomorrow, I’ll miss my flight.
We can think of this as saying: on all occasions in which my alarm didn’t go off, I would miss my flight. This is so, anyway, on all the normal occasions that are likely to arise. We can then draw a picture of the familiar sort, with the circle containing the occasions where my alarm breaks inside the circle of the occasions on which I miss my flight.
When we commit the fallacy of affirming the consequent (3.3), we are arguing as though being in the larger circle is enough to ensure being in the smaller one. But Y’s location in Figure 27.2.2 on the preceding page shows this is wrong. And when we commit the fallacy of denying the antecedent (3.3), we are arguing as though not being in the smaller circle is enough to ensure not being in the larger one. Again, Y shows that this is invalid. It’s all pretty clear when we stick to dogs and mammals, but we’ll now look at a case that many people find confusing.
The Card Selection Task
One of the exercises in the chapter on conditionals went like this:
Wilbur has a pack of cards, each of which has a letter [either a consonant or a vowel] on one side and a number [either even or odd] on the other. Some of the cards are lying flat on a table (Figure 27.2.3). Which cards should you turn over to test the hypothesis:
Hypothesis: If a card has a vowel on one side, then it has an odd number on the other.
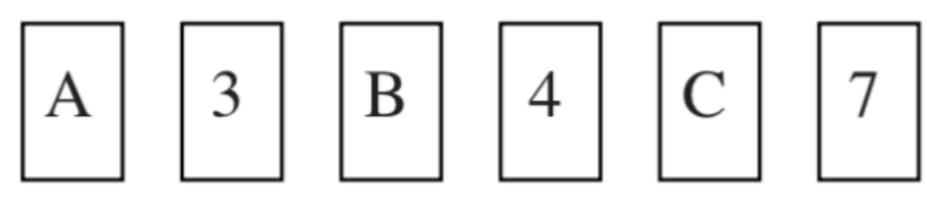.png?revision=1&size=bestfit&width=524&height=112)
Hint: only two of the four kinds of labels are relevant. The problem can be confusing, but once we draw a picture that represents the hypothesis, things become easier. The hypothesis means that if any card has a vowel on one side then it has an odd number on the other, so it’s claiming that all cards with vowels on one side have odd numbers on the other. And we know how to draw a picture of this, which we do in Figure 27.2.4.
.png?revision=1&size=bestfit&width=291&height=270)
Note that the hypothesis only says that all vowels have odd numbers on the other side. It does not say anything about what odd numbers have on the other side, and it does not say anything about what consonants have on the other side. This means that there is no point in flipping either of these sorts of cards. Suppose that I do flip a card with an odd number. Will it matter what is on the other side? No, because our hypothesis doesn’t make any prediction about that. No matter what is on the other side, it’s compatible with the hypothesis.
But what about cards that have even numbers on them? Those are the ones lying outside the big circle in Figure 27.2.3, out in areas like those occupied by the three stars (***). We can see that cards out here cannot be vowels. So, we do need to flip cards out here (which all have even numbers face up). If a card out here has a vowel on it, the hypothesis we are testing is false.
We can also use the diagram to explain the answer in terms of necessary and sufficient conditions. The hypothesis says that having a vowel on one side is sufficient for having an odd number on the other. So, we need to flip each vowel card, and if we find even one without an odd number on the other side, the claim is false. Similarly, the hypothesis says that having an odd number on one side is a necessary condition for having a vowel on the other. So, if we find just one even card with a vowel on the other side, the claim is false. We can see from our picture that the hypothesis requires that if a card is not odd (= even), then it is not a vowel. If we find a card, say ***, that is not odd but is a vowel, the hypothesis is false. The relevant argument pattern here is denying the consequent.
There is some evidence that people are better at problems like this when they involve rules and obligations. We do much better if you ask us which people a policeman must check to see if everyone is obeying the rule:
- Rule: If you buy beer, you must be at least twenty-one.
What is the answer? Why might we do better with problems like this?
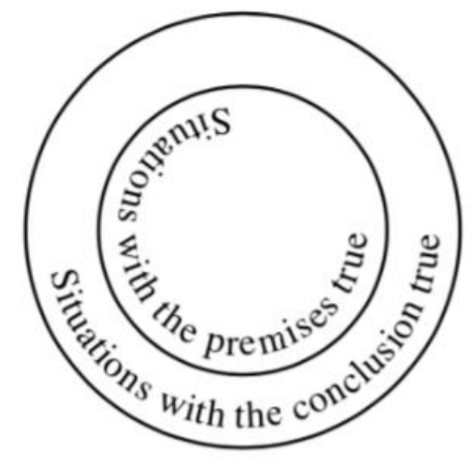
Picturing Validity
.png?revision=1&size=bestfit&width=276&height=272)
An argument is valid just in case it is impossible for all its premises to be true while its conclusion is false. This means there is no way all the premises could be true and the conclusion false. So, in every possible situation in which all the premises are true, the conclusion must be true as well.
We can draw a picture of this by representing the set of all the possible situations in which the premises are true by the inner, smaller circle in Figure 27.2.5 on the preceding page and the set of all the situations in which the conclusion is true by the larger, outside circle.
By contrast, if an argument is invalid, there is some possible scenario in which the premises are true and the conclusion is false. Of course, the definition of validity allows for the conclusion to be true in additional situations in which one or more premises are false.


