11.4.3: 3-Valued Logic

Here is an old argument called the paradox of the heap. Start with a single grain of sand. One grain of sand isn't a heap of sand. Adding one grain to that pile won't make a heap either. In fact, adding one grain of sand to anything that's not a heap does not make it a heap. So, there are no heaps of sand.

But of course there are heaps of sand, so there must be some problem with the reasoning. In wrestling with the logic of vagueness, a small number of logicians suggest that there must be some precise point where the non-heap becomes a heap. Many others recommend using what we call a 3-valued logic to allow some piles to be heaps, some not to be heaps, and some others to be in between. These logicians recommend saying that in these in-between cases the sentence "That is a heap" is neither true nor false, and should be assigned a third truth-value "neither." Let’s indicate this third truth-value with the symbol "#" and assign it to the sentence "Adding one grain of sand to anything that's not a heap does not make it a heap" for the reason that the sentence is not quite true but not quite false either. Maybe we can solve the paradox of the heap this way.

Before we say more about heaps, let’s develop our formal logic a bit more.

Regarding negation, our intuitions tell us that, if P were to abbreviate any formal statement such as A, B, C,..., or even more complicated statements containing many capital letters, then

~P is true iff P is false,

and we expect negation's truth table to have these two rows:

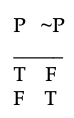
Most philosophers and logicians are happy with this. However, our intuitions are not so clear when it comes to negating a sentence that we believe does not have a classical truth-value (a T or F). Here is why. The philosopher and logician Bertrand Russell believed all sentences do have a classical truth-value, but many advocates of 3-valued logic have the intuition that the following sentence is yet another kind of sentence that is neither true or nor false:

The present king of France is bald.

They say it is neither true nor false because of the failed presupposition, so it should get a third truth-value such as #. They say the negation

The present king of France is not bald

isn't true or false either.

The king of France

Russell again disagrees and says both these sentences about the king of France are false, and they aren't really negations of each other. Anyway, that is why the advocates of 3-valued logic give the following table for negation, where # is the third truth-value that stands for a lack of a classical truth-value:

The Polish logician Jan Łukasiewicz used that table in 1924, but his motivation for developing 3-valued logic was not to give the third truth-value to sentences with failed presuppositions nor to vague sentences but to give it to sentences about the future, such as "There will be a sea battle tomorrow," which he believed were incapable of being assigned either a T or F because tomorrow hasn't happened. Other logicians want to use 3-valued logic for sentences about unreal entities such as "Superman and Batman are having lunch."

To have a full sentential logic that is 3-valued we need to give truth tables for the connector symbols & and v and →. Logicians have investigated various choices for these tables. Let's use the following tables that were recommended by Łukasiewicz.

The way to read these tables for, say A&B is that A's truth-values comes from one of the rows, but B's truth-value comes from one of the columns, and the value of A&B is the value where the A row meets the B column. For example, if A is # and B is F, then we look at the # row and the F column and find that A&B is F.

Exercise \(\PageIndex{1}\)

If the sentence "The present king of France is bald" is given the truth-value #, what is the truth-value of these three sentences when translated into our 3-valued sentential logic?

The present king of France is bald or not bald.
If the present king of France is bald, then the present king of France is bald.
It's not the case that the king of France is both bald and not bald.

Answer

Let B be the sentence "The present king of France is bald." Then the questions are asking for the truth-values of B v ~B and B → B and ~(B & ~B). Their values are required by the truth tables to be # and T and #.

Exercise \(\PageIndex{1}\)

Let's consider a more general question about how 3-valued logic works. Can you s how that Aristotle's law of excluded middle P v ~P holds in classical 2-valued logic but not in our 3-valued logic? The law implies that no matter what truth-value the sentence substituted for P has, the complex sentence P v ~P will have the truth-value T. Why does this implication hold in 2-valued logic but fail in our 3-valued logic?

Answer

Briefly, the law of excluded middle fails in 3-valued logic because, whenever P gets the value #, the bigger sentence P v ~P is not true; it is #.

The previous Concept Check showed that P v ~P is a tautology in our 2-valued logic but fails to be a tautology in our 3-valued logic, as we'd expect. Łukasiewicz wanted it to fail when P was a sentence lacking a classical truth-value such as, "There will be a sea battle tomorrow."

Let's now turn from single sentences to arguments. We define an argument to be deductively valid in either 2-valued or 3-valued logic if and only if its conclusion is true whenever its premises are all true. Arguments in 3-valued logic can be assessed with truth tables in a manner similar to the usual 2-valued logic, but now there are more rows because there are more combinations of truth-values. For example, if an argument is made of sentences from exactly two sentence letters A and B, then instead of the four rows of classical truth tables there are nine rows. You will need the following nine rows in order to treat all the possible assignments of truth-values to the sentence letters A and B:

Let's use truth tables to decide whether the following argument form is valid in our 3-valued logic. It is valid in 2-valued logic and is said to have the logical form called “modus ponens.”

Here is the truth table for that argument in our 3-valued logic:

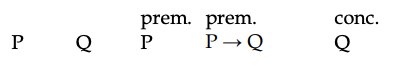
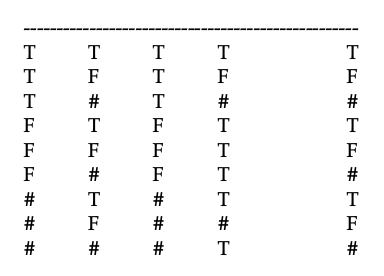
To use this table to assess argument validity, you will look for a row that serves as a counterexample to the argument, namely a row in which the two premises are true but the conclusion is not. There is only one row in which the two premises are true, the first row, so you don't need to look at the other rows. In that first row, Q gets the value T, so the row fails to be a counterexample. Therefore, the argument is valid in 3-valued logic. One moral here is that if you focus in this problem on finding just a counterexample, you don’t need to build the whole nine-row truth table; it is sufficient to build just the first row. Usually in treating any argument there will be some way to streamline the hunt for a counterexample and avoid building large tables.

Exercise \(\PageIndex{1}\)

Show that this classically valid argument is invalid in our 3-valued logic:

A → B so ~A v B

Answer

In the row in which A and B both get the truth-value #, the premise is true but the conclusion is not, so that row is a counterexample