5: Triads
- Page ID
- 180960
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- A is a three-note chord whose notes can be arranged in thirds. A triad can always be “stacked” so that its notes are either on all lines or all spaces.
- When a triad is stacked in its most compact form in thirds, the lowest note is called the , the middle note is called the , and the highest note is called the .
- There are four qualities of triad. A third is major and its fifth is perfect, while a third is minor and its fifth is perfect. A third is minor and its fifth is diminished, while an third is major and its fifth is augmented.
- In , major triads are represented with capital letters that correspond to the triad’s root. Minor triads have a lowercase “mi” after the letter, diminished triads have a superscript circle (o), and augmented triads have a plus sign (+). You may see other abbreviations in other contexts (a more exhaustive list is given in the Chord Symbols chapter).
- Within major and minor keys, triads have particular qualities that correspond to scale degree. These are the same in every major and minor key, which makes memorizing them useful.
- Triads are identified by their , , and .
A is any combination of three or more pitch classes that sound simultaneously. This chapter focuses on —three-note chords whose notes can be stacked into thirds.
Triads
The three notes of a triad can always be arranged in thirds. Example 1 shows two triads, each written both and . The first triad is on three adjacent spaces, while the second triad is on three adjacent lines. A triad can always be “stacked” so that its notes are either on all lines or all spaces. When a triad is stacked in its most compact form (measures 2 and 4 of Example 1), it looks like a snowperson (see Example 2). Just as a snowperson consists of a bottom, middle, and head, a triad consists of lowest, middle, and upper notes.
Example 1. Two triads, shown melodically and harmonically.

Example 2. A snowperson.

Example 3. A triad with the root, third, and fifth labeled.
Colloquially, when a triad is stacked in this fashion, we might call this “snowperson form,” but the official term is ; this is explored more in the chapter titled Inversion and Figured Bass. As Example 3 shows, the lowest note of a triad is called the root, the middle note is called the third (a generic third above the root), and the highest note is called the fifth (a generic fifth above the root).
Triadic Qualities and Listening to Triads
There are four qualities of triad—major, minor, diminished, and augmented—which are determined by the quality of the intervals from the root to the third and the root to the fifth. These qualities are labeled in Example 4: triad qualities are shown above the staff, the quality of the fifth to the root is given in red to the left of the triad, and the quality of the third is given in blue to the right of the triad. Augmented triads are shown last because the other three types are more common in most classical and popular music.
Note that triads are named for certain important intervals they contain:
- Major and minor triads are named for the quality of their third. (Both have perfect fifths.)
- Diminished and augmented triads are named for the quality of their fifth:
- A diminished triad’s fifth is diminished. (Its third is minor.)
- An augmented triad’s fifth is augmented. (Its third is major.)
Listen carefully to the different qualities of triad in Example 4. It is common to pair expressive qualities with triads when learning what they sound like. You might think of major triads as sounding “happy,” minor triads as “sad,” diminished triads as “scary,” and augmented triads as having a “fantasy” or “mystical” sound.
Example 4. Different qualities of triads.
Chord Symbols
for triads include the letter name of the root and an indication of the triad’s quality, and sometimes the pitch class of the bass voice (meaning the lowest note in the chord, not any particular instrument or voice type).
A chord symbol begins with a capital letter (and, if necessary, an accidental) denoting the root of the chord. That letter is followed by information about a chord’s quality. Open Music Theory will use the following abbreviations.[1]
- Major triad: no quality symbol is added
- Minor triad: lowercase “mi”
- Diminished triad: superscript circle (o)
- Augmented triad: plus sign (+)
For example, the chord symbols C, Cmi, Co, and C+ mean a C major triad, C minor triad, C diminished triad, and C augmented triad, respectively. If the root of the chord has an accidental, include it: for example, B♭mi is the chord symbol for a B♭ minor triad, and F♯o is the chord symbol for an F♯ diminished triad.
Finally, if a pitch class other than the chord root is the lowest note in the chord, a slash is added, followed by a capital letter denoting the pitch class in the . This topic will be explored more in the chapter titled Inversion and Figured Bass. Example 5 first shows C major and C minor triads with their chord symbols (C and Cmi). It then shows how the chord symbol for the C minor triad changes when a note other than C is on the bottom: when E♭ is the lowest note, the chord symbol is Cmi/E♭, and when G is the lowest note, the symbol is Cmi/G.
Example 5. Four triads are shown with chord symbols.
Triad Qualities in Major and Minor
Any note of the major scale can be the root of a triad. As you can see in Example 6, which is in the key of G major, triads built on do, fa, and sol (^1, ^4,(1^, 4^, and ^5)5^) in major keys are major, shown with the capital letter of the triad’s root. Triads built on re, mi, and la (^2, ^3,(2^, 3^, and ^6)6^) are minor, shown with a lowercase “mi” after the capital letter of the root. Triads built on ti (^7)(7^) are diminished; this is shown with a superscript “o” (which you might know as the degree symbol). These triadic qualities do not change in different keys; in other words, the quality of a triad built on do (^1)(1^) will always be major in any major key.
Example 6. Qualities of triads in major keys.
Example 7, in the key of G minor, shows the pattern of triad quality for minor scales. Note that this example contains two triads built on sol (^5)(5^) and two built on te/ti (↓^7(↓7^/^7)7^)—one without the raised leading tone (“natural minor”) and one with the raised leading tone (“harmonic minor”). As you can see in Example 7, triads built on do, fa, and sol (^1, ^4,(1^, 4^, and ^5)5^) (without the raised leading tone) are minor (shown with the lowercase “mi”). Triads built on me, le, and te (↓^3,↓^6,(↓3^,↓6^, and ↓^7)↓7^) (without the raised leading tone) are major. A triad built on sol (^5)(5^) with the raised leading tone is also major. Triads built on re and ti (^2(2^ and ^7)7^) (with the raised leading tone) are diminished (shown with the superscript degree symbol).
Example 7. Qualities of triads built on the minor scale.
Spelling Triads
To build a triad from a chord symbol, you need to be aware of the triad’s and . Complete the following steps:
- Draw the root on the staff.
- Draw notes a third and fifth above the root (i.e., draw a snowperson).
- Think of (or write down) the major key signature of the triad’s root.
- To spell a major triad, write any accidentals from the key signature that apply to the notes of the triad.
- For a minor, diminished, or augmented triad, add additional accidentals to alter the chord’s third and/or fifth when appropriate.
Example 8 shows this process for a D major triad:
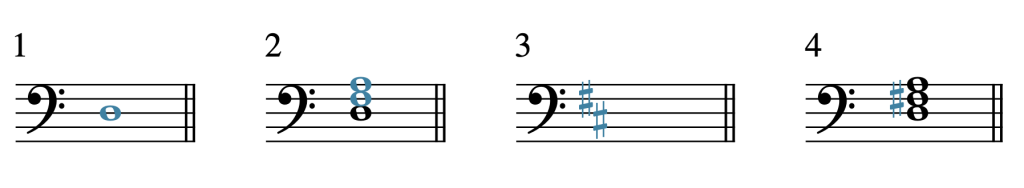
Example 8. Drawing a D major triad in four steps.
- The note D, the chord’s root, is drawn on the staff.
- A snowperson is drawn—an F and A, the notes a generic third and a fifth above the D.
- The key signature of D major has been recalled. D major has two sharps, F♯ and C♯.
- A sharp (♯) has been added to the left of the F, because F♯ is in the key signature of D major. No C♯ was necessary because there is no C in the chord.
Let’s complete this process for an A♭ minor triad (A♭mi), as seen in Example 9.
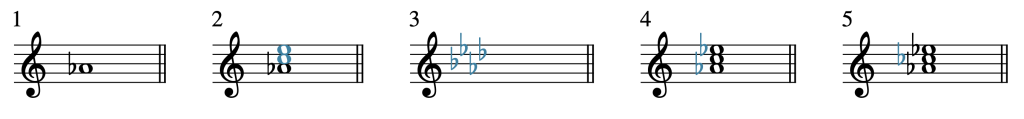
Example 9. Drawing an A♭ minor triad in five steps.
- The note A♭ is written because it is the root of the triad.
- A snowperson is drawn; in other words, the notes C and E are added because they are a generic third and fifth, respectively, above A♭.
- The key signature of A♭ major is recalled. A♭ major has four flats: B♭, E♭, A♭, and D♭.
- E♭ is added, because it is in the key signature of A♭ major. B♭ and D♭ are not needed, because those notes aren’t in an A♭ triad. Now we have successfully spelled an A♭ major triad (A♭, C, and E♭).
- Minor triads contain a minor third, which is one half step smaller than a major third. Therefore, our final step is to lower the chord’s third (the C) by a half step (to a C♭). Now we have an A♭ minor triad (A♭, C♭, and E♭).
Don’t forget that diminished triads have a minor third and a diminished fifth, meaning you have to lower both the third and the fifth by a half step from a major triad. An augmented triad has a major third and an augmented fifth, so its fifth must be raised by a half step from a major triad.
Identifying Triads, Doubling, and Spacing
Triads are identified according to their root, quality, and inversion; inversion is discussed in the Inversion and Figured Bass chapter, so we will focus on root and quality for now. You can identify triads in three steps:
- Identify and write its root.
- Imagine the major key signature of its root.
- Identify and write its quality.
Example 10 shows a triad for the process of identification.
Example 10. A triad for identification.
To identify this triad:
- This triad is written in its most compact form, so the root is the lowest note, D.
- The key of D major has two sharps, F♯ and C♯; we can use this information to identify the quality of the triad.
- In this triad, the F is sharp, matching the major key signature. Therefore, we can correctly identify this as a D major triad.
Let’s apply the same steps to the triad in Example 11:
Example 11. A second triad for identification.
To identify this triad:
- First, we identify and write its root, which is C♯.
- Next, we can identify and write its quality. We imagine the key signature of C♯ major, which has seven sharps (every note is sharp).
- Therefore, E and G would be sharp in the key of C♯ major, but we see that they are both natural in Example 11. Because both the third and the fifth have been lowered by a half step, this triad is diminished. We can now correctly identify this triad as a C♯o triad.
If the bottom note of a triad has an imaginary key signature (because there is a double accidental that applies to it), use enharmonic equivalence to respell the triad. The process for this will be the same as that outlined in the last section of Intervals.
Because of the principle of , the or of notes does not affect a triad’s identification. Example 12 shows several different triads and their chord symbols. As you can see, the identification of these triads is the same, regardless of octave doublings (Example 12a) or the use of with wide intervals (Example 12b). Doublings and open spacing can be combined, as seen in Example 12c. In order to identify triads with doublings and open spacing, you need to either imagine or write the notes as a triad in without any doublings.
Example 12. Doublings do not affect chord symbols.
Online Resources
- Introduction to Chords (musictheory.net)
- Triad Introduction (Robert Hutchinson)
- What is a Triad? (YouTube)
- Building Triads (YouTube)
- Constructing Triads (Columbia)
- Lead-sheet Symbols (Robert Hutchinson)
- Triad Identification Practice Tool (teoria)
- Chord Ear Training (musictheory.net)
- Triad Ear Training (Tone Dear)
- Triad Ear Training (teoria)
Assignments from the Internet
- Triad Identification (.pdf, .pdf, .pdf, .pdf, .pdf, .pdf, .pdf, .pdf)
- Triad Construction (.pdf), pp. 2, 4, 6, 7 (.pdf), p. 9 (.pdf)
Assignments
- Triads Assignment #1 (.pdf, .mcsz)
- Triads Assignment #2 (.pdf, .mcsz)
- Triads Assignment #3 (.pdf, .mcsz)
Media Attributions
- Snowperson © Dustinhart is licensed under a CC BY-NC (Attribution NonCommercial) license
- Root, Third, and Fifth © Chelsey Hamm is licensed under a CC BY-SA (Attribution ShareAlike) license
- d-major © Megan Lavengood is licensed under a CC BY-SA (Attribution ShareAlike) license
- ab-minor © Megan Lavengood is licensed under a CC BY-SA (Attribution ShareAlike) license
- You may see other abbreviations in other contexts (a more exhaustive list is given in the Chord Symbols chapter). ↵

