3.5: Problems with the Square of Opposition
- Page ID
- 24331
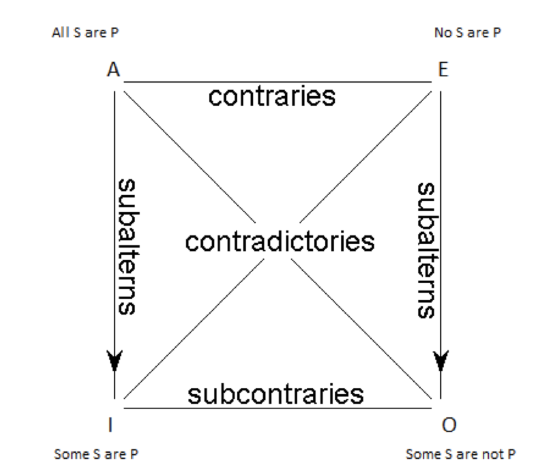
The Square of Opposition is an extremely useful tool: it neatly summarizes, in graphical form, everything we know about the relationships among the four types of a categorical proposition.
Except, actually, we don’t know those things. I’m sorry, but when I first presented the Square of Opposition and made the case for the various relationships it depicts, I was leading you down the proverbial primrose path. What appeared easy is in fact not so simple as it seems. Some of the relationships in the Square break down under certain circumstances and force us to do some hard thinking about how to proceed. It’s time to explore the “steep and thorny way” that opens before us when we dig a bit deeper into problems that can arise for the Square of Opposition.
Existential Import
To explain what these problems are, we need the concept of existential import (E.I. for short). E.I. is a property that propositions may or may not have. A proposition has existential import when its truth implies the existence of something. Because of what we decided to mean when we use the word ‘some’—namely, ‘there is at least one’—the particular propositions I and O clearly have E.I. For ‘Some sailors are not pirates’ to be true, there has to exist at least one sailor who is not a pirate. Again, that’s just a consequence of what we mean by ‘some’.
In addition, given the relationships that are said to hold by the Square of Opposition, the universal propositions A and E also have existential import. This is because the particular propositions are subalterns. The truth of a universal proposition implies the truth of a particular one: if an A is true, then the corresponding I must be; if an E is true, then the corresponding O must be. So since the truth of universals implies the truth of particulars, and particulars have E.I., then universals imply the existence of something as well: they have existential import, too.
Problems for the Square
OK, all four of the categorical propositions have existential import. What’s the big deal? Well, this fact leads to problems. Consider the proposition that all C.H.U.D.s are Republicans; also, consider the proposition that some C.H.U.D.s are not Republicans. Both of these propositions are false. That’s because both of them imply the existence of things—namely, C.H.U.D.s—that don’t exist. (‘C.H.U.D.’ stands for ‘Cannibalistic Humanoid Underground Dweller’. They’re the titular scary monsters of a silly horror movie from the ’80s. They’re not real.) ‘Some C.H.U.D.s are not Republicans’ claims that there exists at least one C.H.U.D. who’s not a Republican; but that’s not the case, since there are no C.H.U.D.s. ‘All C.H.U.D.s are Republicans’ is also false: if it were true, its subaltern ‘Some C.H.U.D.s are Republicans’ would have to be true; but it can’t be, because it claims that there’s such a thing as a C.H.U.D. (who’s a Republican).
Bottom line: A and O propositions about C.H.U.D.s both turn out false. This is a problem for the Square of Opposition because A and O are supposed to be a contradictory pair; they’re supposed to have opposite truth-values.
It gets worse. Any time your subject class is empty—that is, like ‘C.H.U.D.s’, it doesn’t have any members—all four of the categorical propositions turn out false. This is because, as we saw, all four have existential import. But if E and I are both false, that’s a problem: they’re supposed to be contradictory. If I and O are both false, that’s a problem: they’re supposed to be subcontraries. When we talk about empty subject classes, the relationships depicted in the Square cease to hold.
Solution?
So the problems are caused by empty classes. We can fix that. We’re building our own logic from the ground up here. Step one in that process is to tame natural language. The fact that natural language contains terms that don’t refer to anything real seems to be one of the ways in which it is unruly, in need of being tamed. Why not simply restrict ourselves to class terms that actually refer to things, rule out empty classes? Then the Square is saved.
While tempting, this solution goes too far. The fact is, we make categorical claims using empty (or at least possibly empty) class terms all the time. If we ruled these out, our ability to evaluate arguments containing such claims would be lost, and our logic would be impoverished.
One field in which logic is indispensable is mathematics. Mathematicians need precise language to prove interesting claims. But some of the most interesting claims in mathematics involve empty classes. For instance, in number theory, one can prove that there is no largest prime number—they go on forever. In other words, the term ‘largest prime number’ refers to an empty class. If our logic ruled out empty class terms, mathematicians couldn’t use it. But mathematicians are some of our best customers!
Also, physicists. Before its existence was confirmed in 2013, they made various claims about a fundamental particle called the Higgs boson. “Higgs bosons have zero spin,” they might say, making a universal affirmative claim about these particles. But before 2013, they didn’t even know if such particles existed. IF they existed, they would have zero spin (and a certain mass, etc.); the equations predicted as much. But those equations were based on assumptions that may not have been true, and so there may not have been any such particle. Nevertheless, it was completely appropriate to make claims about it, despite the fact that ‘Higgs boson’ might be an empty term.
We make universal claims in everyday life that don’t commit us to the existence of things. Consider the possible admonition of a particularly harsh military leader: Deserters will be shot. This is a universal affirmative claim. But it doesn’t commit to the existence of deserters; in fact, it’s very purpose is to ensure that the class remains empty!
So, empty classes have their uses, and we don’t want to commit ourselves to the existence of things every time we assert a universal claim. Ruling out empty classes from our logic goes too far to save the Square of Opposition. We need an alternative solution to our problems.
Boolean Solution
Advocated by the English logician George Boole in the 19th Century, our solution to the problems raised will be to abandon the assumption that universal propositions (A and E) have existential import, allow empty classes, and accept the consequences. Those consequences, alas, are quite dire for the traditional Square of Opposition. Many of the relationships it depicts do not hold when subject classes are empty.
First, the particular propositions (I and O) are no longer subcontraries. Since they start with the word ‘some’, they have existential import. When their subject classes are empty, as is now allowed, they both turn out false. Subcontraries can’t both be false, but I and O can both be false when we allow empty classes.
Next, the particular propositions are no longer subalterns of their corresponding universals (A and E). As we said, the universals no longer have existential import—they no longer imply the existence of anything—and so their truth cannot imply the truths of particular propositions, which do continue to have E.I.
The only two relationships left on the Square now are contradictoriness—between A and O, E and I—and contrariety between the two universals. And these are in conflict when we have empty subject classes. In such cases, both I and O are false, as we’ve said. It follows that their contradictories, A and E, must be true. But, A and E are supposed to be a contrary pair; they can’t both be true. So we can’t keep both contrariety and contradictoriness; one must go. We will keep contradictoriness. To do otherwise would be to abandon the plain meanings of the words we’re using. There’s a reason I introduced this relationship first: it’s the easiest to understand. If you want to contradict my universal affirmative claim that all sailors are pirates, you claim that some of them aren’t; A and O are clearly contradictory. As are E and I: if you want to contradict my claim that no surfers are priests, you show me one who is. So we eliminate contrariety: it is possible, in cases where the subject class is empty, for both A and E propositions to be true.
What we’re left with after making these revisions is no longer a square, but an X. All that remains is contradictoriness:
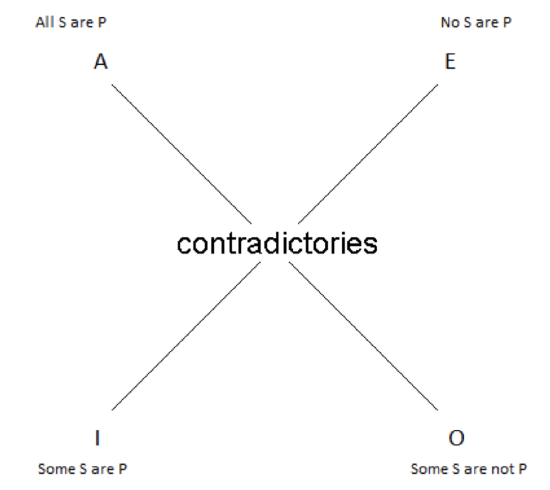
And our solution is not without awkwardness. In cases where the subject class is empty, both particular propositions (I and O) are false; their universal contradictories (E and A), then, are true in those circumstances. This is strange. Both of these sentences express truths: ‘All C.H.U.D.s are Republicans’ and ‘No C.H.U.D.s are Republicans’. That’s a tough pill to swallow, but swallow it we must, given the considerations above. We can make it a bit easier to swallow if we say that they’re true, but vacuously or trivially. That is, they’re true, but not in a way that tells you anything about how things actually are in the world (the world is, after all and thankfully, C.H.U.D.-free).
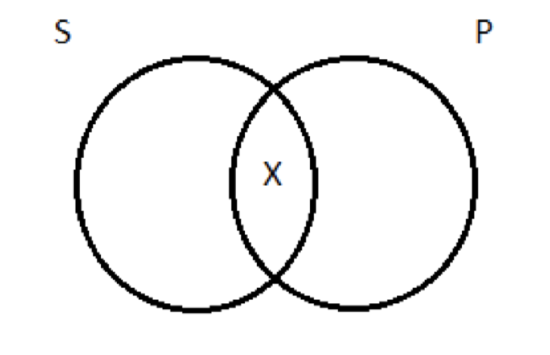
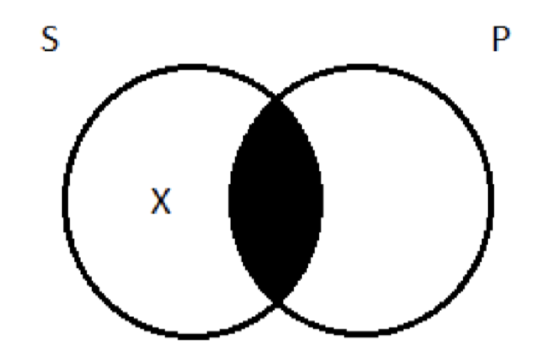
That we would end up choosing this interpretation of the categoricals, rather than the one under which universal propositions had existential import, was foreshadowed earlier, when we first introduced the four types of categorical proposition and talked about how to diagram them. We chose diagrams for A and E that did not imply the existence of anything. Recall that our way of indicating existence in Venn diagrams is to draw an X. So for a particular affirmative—some surfers are priests, say—we drew this picture (with the X being the one surfing priest we’re committed to the existence of):
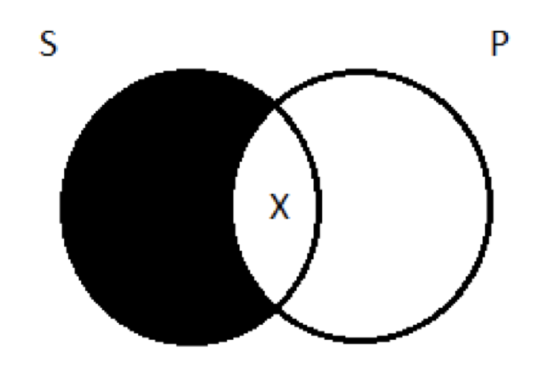
The diagrams for the universals (A and E), though, had no Xs in them, only shading; they don’t commit us to the existence of anything. If we were going to maintain the existential import of A and E, we would’ve drawn different diagrams. For the universal affirmative—all logicians are jerks, say—we’d shade out the portion of the left-hand circle that doesn’t overlap the right, to indicate that there’s no such thing as a logician who’s not a jerk. But we would also put an X in the middle region, to indicate that there is at least one logician who is (existential import):
And for the universal negative—no women are priests, say—we would shade out the middle region, to indicate there’s nothing that’s both a woman and a priest. But we would also put an X in the left-hand circle, to indicate that there’s at least one woman who’s not a priest:
This interpretation of the universal propositions, according to which they have existential import, is often called the “Aristotelian” interpretation (as opposed to our “Boolean” interpretation, according to which they do not). (It is not clear, however, that it is correct to attribute this view to Aristotle. While he clearly did believe that universal affirmative (A) propositions had existential import, it’s not clear that he thought the same about universal negatives. His rendering of the particular negative (O) was ‘Not all S are P’, which could be (trivially, vacuously) true when S is empty. In that case, O’s being the subaltern of E does not force us to attribute Existential Import to the latter. For discussion, see Parsons, Terence, "The Traditional Square of Opposition", The Stanford Encyclopedia of Philosophy (Summer 2015 Edition), Edward N. Zalta (ed.), URL = <http://plato.stanford.edu/archives/s...ntries/square/>) Which interpretation one adopts makes a difference. There are some arguments that the two interpretations evaluate differently: on the Aristotelian view, they are valid, but on the Boolean view, they are not. We will stick to the Boolean interpretation of the universals, according to which they do not have existential import.


