12.2: Using Venn-Euler Diagrams to Test for Invalidity
- Page ID
- 22035
In class logic, we can create diagrams to help us test arguments for validity. Before we do this, though, let’s improve our skill at reasoning with the complement of classes, that is, the set of all things not in a class. If you’re an American, then what’s our name for the non-Americans? It’s “foreigner.” The more Americans travel, the more they meet non-Americans.
Assuming that nobody can be both a Jew and a Christian, it would be true to say that all Jews are non-Christians and true to say that some non-Jews are non-Christians, but it would be false to say that all non-Christians are Jews and false to say all non-Christians are non-Jews. Whew! Congratulations and compliments if you could carefully comprehend the complexities of those complementations about classes. If you could, you can complete this concept check correctly.
Martin (pictured above) is not a white male if Martin is
a. a white non-male.
b. a non-white male,
c. a non-white non-male.
d. any of the above.
- Answer
-
Answer (d). Answering questions like this would be so much easier if we had some sort of picture or diagram method that would show us what is going on. Maybe you can invent one. Euler tried to do this back in the 18th century in Switzerland.
Skill at negating terms is needed for constructing Venn-Euler diagrams. This diagramming method is a helpful way to quickly assess the deductive validity of arguments in class logic. It can guide you to the correct assessment when the argument is too intricate to analyze in your head. In presenting this method, we shall first introduce the diagrams for classes, then generalize the method so that it can be used to display whether sentences about classes are true or false, and then generalize the method again so that it can be used to show whether arguments using these sentences are deductively valid.
The circle below is Euler’s diagram of the class of apples.
r
In this two-dimensional diagram, any point within the circle represents an apple and any point outside the circle represents a non-apple such as a Muslim or a pencil. The custom for labeling is to use a capital to start the name of a region (class) and a small case letter to name a specific member of a region (class). The small letter “r” labels the point to the right of the circle that represents a specific non-apple, let’s say Thomas Edison, the American inventor and founder of the General Electric Corporation. There is nothing important about the shape of the region. An ellipse or a rectangle would be fine, just as long as it is clear what is in the region and what is out, that is, what is in the class and what is not. The size of the circle isn't important either. Nor do we pay attention to moving the diagram to the left or right or up or down. All those changes would produce the same diagram, as far as class logic is concerned.
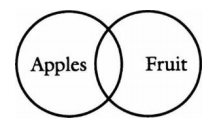
The following is a more complicated diagram that represents both the class of apples and the class of fruit. In the real world, the class of apples is included wholly within the larger class of fruit. The diagram provides a picture of this real-world relationship:
The above diagram represents the truth of the sentence “All apples are fruit,” but you are welcome to draw diagrams that don’t picture the way the world is.
Any label for a region can be inside or outside it, provided there is no ambiguity about which label goes with which region. Sometimes we will call oval regions "circles" since we don’t pay any attention to the difference between a circle and an ellipse.
Here is an Euler diagram in which statements of the form "No A are B" are true:
What is important about this diagram is that the two circles do not intersect (overlap). The circles shouldn't be tangent either, because that would make it hard to tell whether the two classes have a common member.
Here is a Venn diagram showing the same information, but less intuitively:
In a Venn diagram, all circles must mutually overlap. This is not required with Euler diagrams. Consider the points x, y, and z in the following diagram. The classes A and B intersect—that is, they have members in common. One of those members is y.
Point x is neither in class A nor in class B. It’s in the complement of each. Point y is in both A and B. Point z is in B but not in A. By viewing the diagram, you can see that some members of B are in A and some aren't. However, you cannot tell whether A has more members than B. If region A is larger than B in a diagram, you can't tell whether A has more members than B. For that matter, you can't even tell whether the class has any members at all. However, in all diagrams from now on, we will assume that we are starting with classes that are not empty.
Here is a diagram representing the real-world relationship among apples, fruits, oranges, apples in Paris, apples in restaurants in Paris, and fruit owned by our friend Juan:
To be clear, we shall always use capital letters or capitalized words for classes of things. If we want to add the information that some specific object is a member of one of the classes, we will use a lowercase letter to represent the member. In the previous diagram the lowercase a represents the one apple in my refrigerator. You can see that the letter a is outside the P circle; this shows that the apple in my refrigerator is not in Paris. Notice that Juan himself is not a member of any of the classes in the above diagram; the information about Juan is embedded in the definition of J. By inspecting the diagram you can tell that Juan doesn't own any Parisian apples (because J and P do not overlap), but he does own apples (because J intersects A), does own oranges (because J intersects O), and does own some other unspecified fruit (because J is in F but not all of J is in A or O).
Let A = U.S. citizens who live in New York City, B = city dwellers, C = Americans. Here is an Euler diagram displaying their real-world relationships.
Here is how to display the same relationships with a Venn diagram:
In Venn diagrams, shaded areas are the empty set; they contain nothing. With the Venn technique applied to three sets, the three circles must be mutually intersecting, unlike with Euler diagrams.
How would you draw a diagram in which the statement that some apples are from Canada and some aren't is true? This will do the trick:
C = the class of things from Canada
A = the class of apples
The sentence pattern "All A are non-B" is true in the following diagram:
Notice that it is the same as the diagram you’d draw for "No A are B.” Logically equivalent sentences have the same kinds of diagrams. That’s a key idea in class logic.
The above diagram would represent the false sentence "No Texans are Americans" if the following dictionary were used:
A = Texans
B = Americans
Although that sentence is false in the real world, the diagram shows how the world would be if the sentence were true. The same point is made by saying that the diagram is a picture of what is true in a certain "possible world" that isn't the actual world.
Make the statement "All Texans are non-Americans" be true in a diagram, using the above dictionary for A and B.
- Answer
-
Notice that in this diagram every Texan A is outside America B and thus is a nonAmerican. So this possible world isn’t the actual world.
Letting A be the class of apples. In the two diagrams below the sentence "All apples are bananas" is true (even though the sentence is false in the real world):
But notice the difference in the two diagrams. In the one on the left some bananas fail to be apples. This is not so in the diagram on the right. In the second diagram, the class of apples and the class of bananas are the same class. A diagram of the real-world relationships between apples and bananas would instead look like this:
Draw a diagram for apples and fruit in which the following sentence isn't true in the diagram: "All apples are fruit." The sentence is true in the real world, but it won't be in the possible world represented by your diagram.
- Answer
-
There is more than one kind of diagram that will work.
With a sentence such as "All apples are fruit," the analyst has the option of treating it in class logic or in sentential logic. In class logic, it is logically equivalent to "All things in the class of apples are also things in the class of fruit." This states a relationship between two classes. In sentential logic, the sentence is logically equivalent to "If it's an apple, then it's a fruit." This states a conditional relationship between two sub-sentences.
We can now generalize the diagram method to a technique for assessing the deductive validity of arguments, provided that the sentences constituting the argument describe how classes of objects are related to each other. The Venn-Euler diagram method of assessing arguments works only for deductive arguments in class logic. It shows an argument to be valid if there is no diagram of a counterexample to the argument. By definition, the counterexample to an argument is a possible situation or an interpretation of the argument showing how it could have true premises and a false conclusion.
More specifically, here is how to apply the method of checking for validity in class logic:
Translate the premises and conclusion of the argument into appropriate sentences of class logic. Search for a counterexample. That is, try to diagram these sentences in class logic so that the premises come out true in the diagram and the conclusion comes out false in the diagram. If there is a diagram like this, then this counterexample diagram shows that the argument is deductively invalid. However, if all possible diagrams fail to produce a counterexample, then the argument is declared to be deductively valid.
This method never gives an incorrect answer if you have actually correctly examined all possible diagrams. An argument is valid if there exists no counterexample, not merely if you can’t find one. Maybe you can’t find one because you didn’t look carefully. So, the application of the method of Venn-Euler diagrams is risky since its answer depends on you being correct when you say you’ve looked and are confident that no counterexample exists.
To see the technique in action, let’s try it out on this argument pattern:
No A are B.
No C are B.
So, No A are C.
Here is a diagram that makes all the premises be true:
None of the circles intersect or are contained within another. In this diagram the conclusion is true. Can we conclude that the argument pattern is valid? No, not from this information. We should instead have been searching to make sure that there is no diagram that makes the premises true but the conclusion false. In fact, there is such a diagram:
Here the conclusion is false when the premises are true, a telltale sign of invalidity. Therefore, the diagram method declares the argument pattern to be invalid.
Use the diagram method to show the validity of this argument pattern:
All A are B.
All B are C.
So, All A are C.
- Answer
-
Here is a way to draw a diagram of both the premises being true
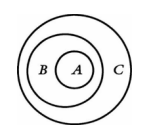
There can be other diagrams of the premises: permit circle A to equal circle B, or for B to equal C. However, in all the possible diagrams of the premises, the conclusion comes out true in the diagram. So, no counterexample can be produced. Therefore, the Venn-Euler technique declares this argument pattern to be valid.
Use the diagram technique to assess the validity or invalidity of this argument. Interpret some to mean "at least one and perhaps all."
Some cats are felines.
Some animals are felines.
So, some animals are cats.
- Answer
-
The argument is invalid; the following diagram serves as a counterexample:
Some C are F.
Some A are F.
Some A are C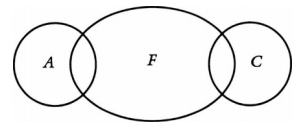
When trying to find the logical form of an argument, it is not always possible to tell whether you should look for its form in class logic or in sentential logic. Experiment to see what will work. Some arguments have logical forms that cannot be expressed adequately either way, and then more powerful logics such as predicate logic must be brought to bear on the argument.
In addition, some arguments are deductively valid although their validity is not a matter of logical form using any formal logic. Here is an example:
John is a bachelor.
So, he is not married.
The validity is due not just to form, but to content—in particular, to the fact that the definition of bachelor implies that all bachelors are not married. We could force this argument to be valid due to its logical form in class logic if we could encode the idea that all bachelors are not married into class logic, and we can. Just add the premise: All bachelors are not married. Valid arguments that don’t need the insertion of definitions are called formally valid. All formally valid arguments are deductively valid, but the reverse doesn't hold. However, in our course we won’t pay attention to this fine distinction. If you see that a definition is needed to make the argument be valid, go ahead and insert it and don’t worry about the fact that this shows your argument is deductively valid but not formally valid.
Venn-Euler diagrams have other uses besides checking for validity. If two sentences can have the same diagram, then they are logically equivalent in class logic. The diagrams also can be used to check for consistency. If there is a diagram in which each sentence in a set of sentences comes out true, then the set is logically consistent.


