12.1: Aristotle's Logic of Classes
- Page ID
- 22034
A class is any collection, group, or set that is thought of as a single object. All the black symbols on your computer screen make a class, and so do all your fingers. You could even mentally collect these two classes into the combination class of both kinds of things, although that would be a very odd class. Surprisingly much ordinary talk that does not seem to be about classes can be interpreted so it is explicitly about classes, and that is why class logic is more useful than it might appear to be at first. For example, saying Obama is a president can be interpreted as saying Obama is in the class of presidents. He’s a member of that class.
Class logic focuses on the classes that are mentioned in subjects and predicates of sentences, and it focuses on the occurrence of the key words all, some, none and their synonyms. For example, the word Greek refers to the class of Greeks, and the sentence "All Greeks are Europeans" can be interpreted as saying that the class of Greeks is included within the class of Europeans─that is, any member of the class of Greeks is also a member of the class of Europeans. The sentence "Socrates was an ancient Greek" does not seem to be about classes, but it can be interpreted as saying that one object (namely, Socrates) is a member of a class (namely, the class of ancient Greeks). In class logic, the sentence "No Americans are Europeans" would be interpreted as saying that the class of Americans does not overlap with the class of Europeans─that is, the two classes do not have a member in common.

Sentences about classes have logical forms. For example, the sentence "Some Europeans are Greek" has the form "Some E are G" where the letter E stands for the class of Europeans and the letter G stands for Greeks. The sentence is interpreted in class logic as asserting that some members of E are members of G. The statement form "All N are B" is a briefer version of "All members of the class N are members of the class B.” In sentential logic, the capital letters were used for sentences or clauses, but here in Aristotle’s class logic, the capital letters are used for classes.
Just as sentences have logical forms, so do arguments.

Here is an argument that can be paraphrased in English to reveal its class structure:
Nazis are bad.
Nazis like to beat up Catholics.
So, liking to beat up Catholics is bad.
Its paraphrase in class logic:
All members of the class of Nazis are members of the class of bad persons.
All members of the class of Nazis are members of the class of persons who like to beat up Catholics.
So, all members of the class of persons who like to beat up Catholics are members of the class of bad persons.

In creating a paraphrase for use in class logic, we search for logically equivalent sentences in which the main verb is some form of to be and in which the subject and predicate can be read as being about classes. Using some obvious abbreviations of the classes, we can display the logical form of the above argument as follows:
All N are B
All N are L.A
ll L are B.
where
N = (the class of) Nazis
B = (the class of) bad persons
L = (the class of) all persons who like to beat up Catholics
The test of whether we have actually found the logical form of the argument is whether we can reproduce the argument by substituting the words back in for the letters.
Two different arguments in English might have the same form in class logic if we can change the definition of the capital letters. For example, if the letter L were to stand for the class of persons who like to breathe air, then on substituting words for letters in the above argument form, we would get an analogous argument about Nazis liking to breathe air.
Nazis are bad.
Nazis like to breathe air.
So, liking to breathe air is bad.
The two arguments rise and fall together in class logic because they are logically analogous—that is, they have the same form in class logic. This particular form is deductively invalid, isn’t it?
Our choice of the letter N was arbitrary. We can re-letter formal arguments in class logic and get the same form. If we replaced N with M above, we’d get this analogous form:
All M are B
All M are L.
All L are B.
In class logic, if we are talking about individual members rather than classes, the custom is to use small case letters. So, if we wanted to treat the sentence “The biggest fish in our sea is not a mammal” in class logic, we might choose the small case letter “b” for “the biggest fish in our sea” and choose “M” for the predicate “is a mammal.” Then we’d translate our sentence into class logic as “b is NOT-M.”
The “NOT” isn’t the negation that was used in sentential logic. Here it means the complement of M, that is, the class of all things not in M.
Which one of the choices below has the logical form of this argument about whales? (Hint: The order in which the premises are presented in an argument is not essential to an argument's validity or to its form.) Whales are mammals, but the biggest fish in our sea is definitely not a mammal, so it's not a whale either.
- Potatoes are produce. Not all fattening foods are potatoes, so not all fattening foods are produce either.
- That squirming thing has no backbone. However, fish are the kind of things that do have backbones. So it's not a fish.
- Fat fish are swimmers. No house cat is a fat fish, so no house cats are swimmers.
- Answer
-
Answer (b). Both arguments have this form: All W are M. b is NOT-M, so b is NOT-W.

You aren’t restricted to using single capital letters for a class. If it helps you remember its name better by giving the class a longer name, that is OK. You could have chosen “MAM” as the abbreviation of the class of mammals instead of “M.”
Choose the correct class logic pattern for the following biological argument:
All insects have exactly six legs. So no spider is an insect because all spiders have exactly eight legs.
Here are four choices for the pattern. SIX stands for the class of things that have six legs.

- Answer
-
Answer (d). Only (b) and (d) have the correct conclusion below the line
The two arguments below have different forms. Any argument with the form on the right is valid:
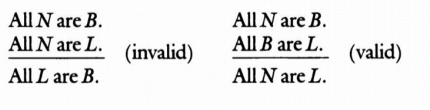
You should be able to think of a counterexample to the argument form on the left. Think about what definitions you could give to N, B and L that would create an argument with true premises and a false conclusion.
Substituting Nazis for N and bad people for B and like to breathe air for L will produce a counterexample to the form on the left.
If some A are C and all C are R, then must some R be A?
- Answer
-
Yes, this is deductively valid reasoning in class logic. You cannot think of any definitions for the letters that will produce an invalid argument.
From the answer to the previous concept check you can see that deductive logic is placing limits on what you can think of.

Is this a deductively valid argument form?
No A are B.
Some B are C.
No A are C.
- Answer
-
No, it is deductively invalid. You can probably think of some definitions for the letters that will produce an invalid argument. How about A being apples and B being bananas and C being fruit?


