11.4.1: Truth Tables

Let's develop what is called the formal semantics of Sentential Logic. Semantics is about, among other things, the way the truth of some sentences affect the truth of other sentences. Truth and falsehood are said to be the two truth-values that sentences can have. But a sentence can't have both of them at the same time.

Here is the truth table that gives a picture of how negation works:

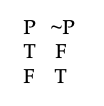
This table implies, among other things, that (A & B) and ~(A & B) have opposite truth-values, as you can see by letting P abbreviate "(A & B)" in the truth table.

Here is a truth table for how 'v' affects a sentence's truth-values:

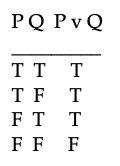
The last line of this table implies that if sentence A (when substituted for P) were false and sentence B (substituted for Q) were false, then sentence A v B would have to be false. But the table doesn't apply just to simple sentence letters. The last line also implies that if sentence C & A is false and sentence C & B is false, then sentence (C & A) v (C & B) is false, too.

Here is the truth table for &

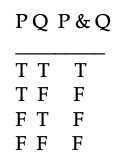
The &-table tells you that the only way for an & sentence to be true is for both of its component sentences to be true. For example, the only way for (A v B) & (C v A) to be true is for (A v B) to be true and (C v A) to be true.

Here is the truth table for →

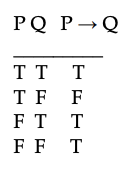
You can build larger truth tables to help you figure out the truth-values of complicated sentences from knowing the truth-values of their component sentence letters. Here is a truth table for (A & (A → B)) → B. The intermediate columns for A → B and for A & (A → B) are our "scratch work" to help us figure out the truth-value of the larger sentence.

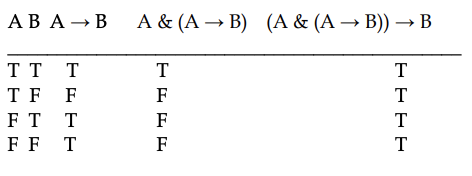
You need a row of a truth table for every way you can assign Ts and Fs to the component sentence letters. If there were a third sentence letter such as C in a formal sentence, then its truth table would need eight rows instead of four. How did we figure out that a T belongs in the last row in the last column in the above table? We made use of the fact that the sentence (A & (A → B)) → B is basically an → sentence whose if-part is F [as we found by doing the scratch work] and whose then-part is F. Then we noticed that the truth table for P→Q says that, when P has the truth-value F and Q has the value F, we should assign T to P→Q. That's why a T belongs in the bottom row in the right column of the table above.

Exercise \(\PageIndex{1}\)

What is the truth-value of E v (F & G) in a row of the truth table where E is false and F and G are both true?

Answer

It is true. If F and G are true, then F&G has to be true. But that makes the right side of the 'v' be true, and the truth table for 'v' then requires the full sentence to be true.

For every sentence of Sentential Logic, no matter how long the sentence is, we can build its truth table in this manner and figure out the conditions (rows) under which it is true and the conditions under which it is false. This feature of Sentential Logic is called the truth functionality of Sentential Logic.

To say a little more about semantics, we can define a logically true sentence or a tautology in Sentential Logic to be a sentence that is true no matter what the truth-values are of its simple letters. For example, A v ~A is a tautology, but A v B is not. A v B might be true or might be false depending what values A and B have. It will come out false if A and B are both false, as you could check by working out the truth table. A sentence that is always false no more what the truth-values are of its simple letters is called a contradiction. A & ~A is a contradiction. Most sentences of Sentential Logic are neither tautologies nor contradictions. We call such sentences contingent. For example, the sentence A v B is contingent. So is C. In some conditions they are true and in other conditions they are false.

Let's go back to English for a moment and compare what we've just said about contingent sentences of Sentential Logic with contingent sentences of English. 4The sentence “President Eisenhower was a general” is contingent because it might be true and might be false. Yet it is actually true; it's not really false. It might be false, not in the sense that it might become false, but only in the sense that it might have been false if the facts of the world had been different. The sentence "President Eisenhower was a general or he wasn't" is a logical truth, and you could figure out that it was true even if you'd never heard of President Eisenhower. There's no way to change the conditions or facts of the world to make this sentence be anything other than true. You figure this out just be looking at its underlying logical form and knowing how "or" and "negation" work in English. Now, suppose there is a person you've never heard of, say Sen-Chu. Do you know whether the following sentence is true?

Sen-Chu was and wasn't a general.

You can tell this is false just because of its semantic structure, of how the words "and" and "not" work. No matter who this Sen-Chu person is, the sentence must be false. This insight you have about semantic structure is reflected in Sentential Logic when you figure out that the complex sentence A & ~A has to be false even if you don't know the truth-value of A.

Exercise \(\PageIndex{1}\)

One of these sentences is a tautology, one is contingent, and one is a contradiction. Which is which?

F & (~F v G)
~F v (B & (B → F))
(C → D) v ~(C → D)

Answer

contingent, contradiction, tautology.

The negation of a sentence p is another sentence q that has the opposite truth-value as p in any situation, that is, in any assignment of Ts and Fs to the basic sentence letters. It is easy to see that ~A is the negation of A.

Two statements are said to be semantically equivalent (or just equivalent) if they agree in their truth-values no matter what the situation, that is, no matter what assignment of Ts and Fs to their basic sentence letters. A is equivalent to ~~A. B is equivalent to B v B. ~A is equivalent to A → (B & ~B).

Exercise \(\PageIndex{1}\)

The sentence C v ~B is equivalent to one and only one of the following sentences. Which one?

a. C → B
b. B → C
c. ~B → C
d. B → ~C
e. ~B → ~C

Answer

b.