1.5: Parmenides and Zeno’s Paradoxes

Parmenides⁸

Parmenides of Elea (/pɑːrˈmɛnᵻdiːz əv ˈɛliə/; Greek: Παρμενίδης ὁ Ἐλεάτης; fl. late sixth or early fifth century BC) was a pre-Socratic Greek philosopher from Elea in Magna Graecia (Greater Greece, included Southern Italy). He was the founder of the Eleatic school of philosophy. The single known work of Parmenides is a poem, On Nature, which has survived only in fragmentary form. In this poem, Parmenides describes two views of reality. In "the way of truth" (a part of the poem), he explains how reality (coined as "what-is") is one, change is impossible, and existence is timeless, uniform, necessary, and unchanging. In "the way of opinion", he explains the world of appearances, in which one's sensory faculties lead to conceptions which are false and deceitful.

Early life

Parmenides was born in the Greek colony of Elea (now Ascea), which, according to Herodotus, had been founded shortly before 535 BC. He was descended from a wealthy and illustrious family.

His dates are uncertain; according to Diogenes Laërtius, he flourished just before 500 BC, which would put his year of birth near 540 BC, but Plato has him visiting Athens at the age of 65, when Socrates was a young man, c. 450 BC, which, if true, suggests a year of birth of c. 515 BC. He was said to have been a pupil of Xenophanes, and regardless of whether they actually knew each other, Xenophanes' philosophy is the most obvious influence on Parmenides. Diogenes Laërtius also describes Parmenides as a disciple of "Ameinias, son of Diochaites, the Pythagorean"; but there are no obvious Pythagorean elements in his thought.

However, according to Sir William Smith, in Dictionary of Greek and Roman Biography and Mythology (1870):

Others content themselves with reckoning Parmenides as well as Zeno as belonging to the Pythagorean school, or with speaking of a Parmenidean life, in the same way as a Pythagorean life is spoken of; and even the censorious Timon allows Parmenides to have been a high-minded man; while Plato speaks of him with veneration, and Aristotle and others give him an unqualified preference over the rest of the Eleatics.

Career

The first hero cult of a philosopher we know of was Parmenides' dedication of a heroon to his teacher Ameinias in Elea. Parmenides was the founder of the School of Elea, which also included Zeno of Elea and Melissus of Samos. Of his life in Elea, it was said that he had written the laws of the city. His most important pupil was Zeno, who according to Plato was 25 years his junior, and was regarded as his eromenos. Parmenides had a large influence on Plato, who not only named a dialogue, Parmenides, after him, but always spoke of him with veneration.

Thought

William Smith also wrote in Dictionary of Greek and Roman Biography and Mythology:

Reason is our guide; on the latter the eye that does not catch the object and re-echoing hearing. On the former path we convince ourselves that the existent neither has come into being, nor is perishable, and is entirely of one sort, without change and limit, neither past nor future, entirely included in the present. For it is as impossible that it can become and grow out of the existent, as that it could do so out of the non-existent; since the latter, non-existence, is absolutely inconceivable, and the former cannot precede itself; and every coming into existence presupposes a non-existence. By similar arguments divisibility, motion or change, as also infinity, are shut out from the absolutely existent, and the latter is represented as shut up in itself, so that it may be compared to a well-rounded ball; while thought is appropriated to it as its only positive definition. Thought and that which is thought of (Object) coinciding; the corresponding passages of Plato, Aristotle, Theophrastus, and others, which authenticate this view of his theory.

Additionally, in the same volume, Smith stated:

Of the cosmogony of Parmenides, which was carried out very much in detail, we possess only a few fragments and notices, which are difficult to understand, according to which, with an approach to the doctrines of the Pythagoreans, he conceived the spherical mundane system, surrounded by a circle of the pure light (Olympus, Uranus); in the centre of this mundane system the solid earth, and between the two the circle of the milkyway, of the morning or evening star, of the sun, the planets, and the moon; which circle he regarded as a mixture of the two primordial elements.

I
The steeds that bear me carried me as far as ever my heart
Desired, since they brought me and set me on the renowned
Way of the goddess, who with her own hands conducts the man
who knows through all things. On what way was I borne

5 along; for on it did the wise steeds carry me, drawing my car,
and maidens showed the way. And the axle, glowing in the socket -
for it was urged round by the whirling wheels at each
end - gave forth a sound as of a pipe, when the daughters of the
Sun, hasting to convey me into the light, threw back their veils

10 from off their faces and left the abode of Night.
There are the gates of the ways of Night and Day, fitted
above with a lintel and below with a threshold of stone. They
themselves, high in the air, are closed by mighty doors, and
Avenging Justice keeps the keys that open them. Her did

15 the maidens entreat with gentle words and skilfully persuade
to unfasten without demur the bolted bars from the gates.
Then, when the doors were thrown back,
they disclosed a widepening, when their brazen
hinges swung backwards in the

20 sockets fastened with rivets and nails. Straight through them,
on the broad way, did the maidens guide the horses and the car,
and the goddess greeted me kindly, and took my right hand
in hers, and spake to me these words: -
Welcome, noble youth, that comest to my abode on the car

25 that bears thee tended by immortal charioteers ! It is no ill
chance, but justice and right that has sent thee forth to travel
on this way. Far, indeed, does it lie from the beaten track of
men ! Meet it is that thou shouldst learn all things, as well
the unshaken heart of persuasive truth, as the opinions of

30 mortals in which is no true belief at all. Yet none the less
shalt thou learn of these things also, since thou must judge
approvedly of the things that seem to men as thou goest
through all things in thy journey."

II

Come now, I will tell thee - and do thou hearken to my
saying and carry it away - the only two ways of search that
can be thought of. The first, namely, that It is, and that it is
impossible for anything not to be, is the way of. conviction,

5 for truth is its companion.. The other, namely, that It is not,
and that something must needs not be, - that, I tell thee, is a
wholly untrustworthy path. For you cannot know what is
not - that is impossible - nor utter it;

III

For it is the same thing that can be thought and that can be.


VI

It needs must be that what can be thought and spoken of is;
for it is possible for it to be, and it is not possible for, what is
nothing to be. This is what I bid thee ponder. I hold thee
back from this first way of inquiry, and from this other also,

5 upon which mortals knowing naught wander in two minds; for
hesitation guides the wandering thought in their breasts, so that
they are borne along stupefied like men deaf and blind.
Undiscerning crowds, in whose eyes the same thing and not the
same is and is not, and all things travel in opposite directions !

VII

For this shall never be proved, that the things that are not
are; and do thou restrain thy thought from this way of inquiry.
Nor let habit force thee to cast a wandering eye upon this
devious track, or to turn thither thy resounding ear or thy

5 tongue; but do thou judge the subtle refutation of their
discourse uttered by me.

VIII

One path only is left for us to
speak of, namely, that It is. In it are very many tokens that
what is, is uncreated and indestructible, alone, complete,
immovable and without end. Nor was it ever, nor will it be; for

5 now it is, all at once, a continuous one. For what kind of origin
for it. will you look for ? In what way and from what source
could it have drawn its increase ? I shall not let thee say nor
think that it came from what is not; for it can neither be
thought nor uttered that what is not is. And, if it came from

10 nothing, what need could have made it arise later rather than
sooner ? Therefore must it either be altogether or be not at
all. Nor will the force of truth suffer aught to arise besides
itself from that which in any way is. Wherefore, Justice does
not loose her fetters and let anything come into being or pass

15 away, but holds it fast.
" Is it or is it not ? " Surely it is adjudged, as it needs must
be, that we are to set aside the one way as unthinkable and
nameless (for it is no true way), and that the other path is real
and true. How, then, can what is be going to be in the

20 future ? Or how could it come into being ? If it came into
being, it is not; nor is it if it is going to be in the future. Thus is
becoming extinguished and passing away not to be heard of.
Nor is it divisible, since it is all alike, and there is no more
of it in one place than in another, to hinder it from holding
together, nor less of it, but everything is full of what is.

25 Wherefore all holds together; for what is; is in contact with what is.
Moreover, it is immovable in the bonds of mighty chains, without
beginning and without end; since coming into being
and passing away have been driven afar, and true belief has cast them away.
It is the same, and it rests in the self-same place, abiding in itself.

30 And thus it remaineth constant in its place; for hard necessity
keeps it in the bonds of the limit that holds it fast on every side.
Wherefore it is not permitted to what is to be infinite; for it is in need of nothing ; while, if it were infinite, it would stand in need of everything. It is the
same thing that can be thought and for the sake of which the thought exists ;

35 for you cannot find thought without something that is, to which it is
betrothed. And there is not, and never shall be, any time other, than that which
is present, since fate has chained it so as to be whole and immovable.
Wherefore all these things are but the names which mortals
have given, believing them, to be true –

40 coming into being and passing away, being and not being,
change of place and alteration of bright colour.
Where, then, it has its farthest boundary, it is complete on
every side, equally poised from the centre in every direction,
like the mass of a rounded sphere; for it cannot be greater or

45 smaller in one place than in another. For there is nothing
which is not that could keep it from reaching out equally, nor
is it possible that there should be more of what is in this place
and less in that, since it is all inviolable. For, since it is equal
in all directions, it is equally confined within limits.

50 Here shall I close my trustworthy speech and thought about the truth.
Henceforward learn the opinions of mortals,
giving ear to the deceptive ordering of my words.
Mortals have settled in their minds to speak of two forms, one of which
they should have left out, and that is where they go astray from the truth.

55 They have assigned an opposite
substance to each, and marks distinct from one another. To the
one they allot the fire of heaven, light, thin, in every direction
the same as itself, but not the same as the other. The other is
opposite to it, dark night, a compact and heavy body. Of these

60 I tell thee the whole arrangement as it seems to men,
in order that no mortal may surpass thee in knowledge.

IX

Now that all things have been named light and night; and the things
which belong to the power of each have been assigned to these
things and to those, everything is full at once of light and dark night,
both equal, since neither has aught to do with the other.

X

And thou shalt know the origin of all the things on high,
and all the signs in the sky, and the resplendent works of the
glowing sun’s clear torch, and whence they arose. And thou
shalt learn likewise of the wandering deeds of the round-faced

5 moon, and of her origin. Thou shalt know, too, the heavens
that surround us, whence they arose, and how Necessity took
them and bound them to keep the limits of the stars . . .

XI

How the earth, and the sun, and the moon, and the sky that is
common to all, and the Milky Way, and the outermost Olympos,
and the burning might of the stars
arose.

XII

The narrower circles are filled with unmixed fire, and those
surrounding them with night, and in the midst of these rushes
their portion of fire. In the midst of these circles is the divinity that directs
the course of all things; for she rules over all painful birth and all begetting,

5 driving the female to the embrace of the male, and the male to that of the female.

XIII

First of all the gods she contrived Eros.

XIV

Shining by night with borrowed light, wandering round the earth.

XV

Always straining her eyes to the beams of the sun.

XVII

On the right boys; on the left girls.

XIX

Thus, according to men’s opinions, did things comp into
being, and thus they are now. In time (they think) they will
grow up and pass away. To each of these things men have
assigned a fixed name.

ZENO’S PARADOXES¹⁰

Zeno's paradoxes are a set of philosophical problems generally thought to have been devised by Greek philosopher Zeno of Elea (ca. 490–430 BC) to support Parmenides' doctrine that contrary to the evidence of one's senses, the belief in plurality and change is mistaken, and in particular that motion is nothing but an illusion. It is usually assumed, based on Plato's Parmenides (128a–d), that Zeno took on the project of creating these paradoxes because other philosophers had created paradoxes against Parmenides' view. Thus Plato has Zeno say the purpose of the paradoxes "is to show that their hypothesis that existences are many, if properly followed up, leads to still more absurd results than the hypothesis that they are one." (Parmenides 128d). Plato has Socrates claim that Zeno and Parmenides were essentially arguing exactly the same point (Parmenides 128a–b).

Some of Zeno's nine surviving paradoxes (preserved in Aristotle's Physics and Simplicius's commentary thereon) are essentially equivalent to one another. Aristotle offered a refutation of some of them. Three of the strongest and most famous—that of Achilles and the tortoise, the Dichotomy argument, and that of an arrow in flight—are presented in detail below.

Zeno's arguments are perhaps the first examples of a method of proof called reductio ad absurdum also known as proof by contradiction. They are also credited as a source of the dialectic method used by Socrates.

Some mathematicians and historians, such as Carl Boyer, hold that Zeno's paradoxes are simply mathematical problems, for which modern calculus provides a mathematical solution. Some philosophers, however, say that Zeno's paradoxes and their variations (see Thomson's lamp) remain relevant metaphysical problems.

The origins of the paradoxes are somewhat unclear. Diogenes Laertius, a fourth source for information about Zeno and his teachings, citing Favorinus, says that Zeno's teacher Parmenides was the first to introduce the Achilles and the tortoise paradox. But in a later passage, Laertius attributes the origin of the paradox to Zeno, explaining that Favorinus disagrees.

Paradoxes of motion

Achilles and the tortoise

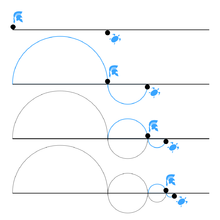
Achilles and the tortoise

In a race, the quickest runner can never overtake the slowest, since the pursuer must first reach the point whence the pursued started, so that the slower must always hold a lead. – as recounted by Aristotle, Physics VI:9, 239b15

In the paradox of Achilles and the Tortoise, Achilles is in a footrace with the tortoise. Achilles allows the tortoise a head start of 100 meters, for example. If we suppose that each racer starts running at some constant speed (one very fast and one very slow), then after some finite time, Achilles will have run 100 meters, bringing him to the tortoise's starting point. During this time, the tortoise has run a much shorter distance, say, 10 meters. It will then take Achilles some further time to run that distance, by which time the tortoise will have advanced farther; and then more time still to reach this third point, while the tortoise moves ahead. Thus, whenever Achilles reaches somewhere the tortoise has been, he still has farther to go. Therefore, because there are an infinite number of points Achilles must reach where the tortoise has already been, he can never overtake the tortoise.

Dichotomy paradox

That which is in locomotion must arrive at the half-way stage before it arrives at the goal.– as recounted by Aristotle, Physics VI:9, 239b10

Suppose Homer wishes to walk to the end of a path. Before he can get there, he must get halfway there. Before he can get halfway there, he must get a quarter of the way there. Before traveling a quarter, he must travel one-eighth; before an eighth, one-sixteenth; and so on.

This description requires one to complete an infinite number of tasks, which Zeno maintains is an impossibility.

This sequence also presents a second problem in that it contains no first distance to run, for any possible (finite) first distance could be divided in half, and hence would not be first after all. Hence, the trip cannot even begin. The paradoxical conclusion then would be that travel over any finite distance can neither be completed nor begun, and so all motion must be an illusion. An alternative conclusion, proposed by Henri Bergson, is that motion (time and distance) is not actually divisible.

This argument is called the Dichotomy because it involves repeatedly splitting a distance into two parts. It contains some of the same elements as the Achilles and the Tortoise paradox, but with a more apparent conclusion of motionlessness. It is also known as the Race Course paradox. Some, like Aristotle, regard the Dichotomy as really just another version of Achilles and the Tortoise.

There are two versions of the dichotomy paradox. In the other version, before Homer could reach the end of the path, he must reach half of the distance to it. Before reaching the last half, he must complete the next quarter of the distance. Reaching the next quarter, he must then cover the next eighth of the distance, then the next sixteenth, and so on. There are thus an infinite number of steps that must first be accomplished before he could reach the end of the path. Expressed this way, the dichotomy paradox is very much analogous to that of Achilles and the tortoise.

Arrow paradox

If everything when it occupies an equal space is at rest, and if that which is in locomotion is always occupying such a space at any moment, the flying arrow is therefore motionless.

– as recounted by Aristotle, Physics VI:9, 239b5

In the arrow paradox (also known as the fletcher's paradox), Zeno states that for motion to occur, an object must change the position which it occupies. He gives an example of an arrow in flight. He states that in any one (duration-less) instant of time, the arrow is neither moving to where it is, nor to where it is not. It cannot move to where it is not, because no time elapses for it to move there; it cannot move to where it is, because it is already there. In other words, at every instant of time there is no motion occurring. If everything is motionless at every instant, and time is entirely composed of instants, then motion is impossible.

Whereas the first two paradoxes divide space, this paradox starts by dividing time—and not into segments, but into points.

Three other paradoxes as given by Aristotle

Paradox of Place

From Aristotle:

if everything that exists has a place, place too will have a place, and so on ad infinitum.

Paradox of the Grain of Millet

Description of the paradox from the Routledge Dictionary of Philosophy:

The argument is that a single grain of millet makes no sound upon falling, but a thousand grains make a sound. Hence a thousand nothings become something, an absurd conclusion.

Aristotle's refutation:

Zeno is wrong in saying that there is no part of the millet that does not make a sound: for there is no reason why any such part should not in any length of time fail to move the air that the whole bushel moves in falling. In fact it does not of itself move even such a quantity of the air as it would move if this part were by itself: for no part even exists otherwise than potentially.

Description from Nick Huggett:

This is a Parmenidean argument that one cannot trust one's sense of hearing. Aristotle's response seems to be that even inaudible sounds can add to an audible sound.

The Moving Rows (or Stadium)

The moving rows

From Aristotle:

concerning the two rows of bodies, each row being composed of an equal number of bodies of equal size, passing each other on a race-course as they proceed with equal velocity in opposite directions, the one row originally occupying the space between the goal and the middle point of the course and the other that between the middle point and the starting-post. This...involves the conclusion that half a given time is equal to double that time.

For an expanded account of Zeno's arguments as presented by Aristotle, see Simplicius' commentary On Aristotle's Physics.

Proposed solutions

Simplicius of Cilicia

According to Simplicius, Diogenes the Cynic said nothing upon hearing Zeno's arguments, but stood up and walked, in order to demonstrate the falsity of Zeno's conclusions. To fully solve any of the paradoxes, however, one needs to show what is wrong with the argument, not just the conclusions. Through history, several solutions have been proposed, among the earliest recorded being those of Aristotle and Archimedes.

Aristotle

Aristotle (384 BC−322 BC) remarked that as the distance decreases, the time needed to cover those distances also decreases, so that the time needed also becomes increasingly small. Aristotle also distinguished "things infinite in respect of divisibility" (such as a unit of space that can be mentally divided into ever smaller units while remaining spatially the same) from things (or distances) that are infinite in extension ("with respect to their extremities"). Aristotle's objection to the arrow paradox was that "Time is not composed of indivisible nows any more than any other magnitude is composed of indivisibles."

Thomas Aquinas

Thomas Aquinas, commenting on Aristotle's objection, wrote "Instants are not parts of time, for time is not made up of instants any more than a magnitude is made of points, as we have already proved. Hence it does not follow that a thing is not in motion in a given time, just because it is not in motion in any instant of that time."

Archimedes

Before 212 BC, Archimedes had developed a method to derive a finite answer for the sum of infinitely many terms that get progressively smaller. (See: Geometric series, 1/4 + 1/16 + 1/64 + 1/256 + · · ·, The Quadrature of the Parabola.) Modern calculus achieves the same result, using more rigorous methods (see convergent series, where the "reciprocals of powers of 2" series, equivalent to the Dichotomy Paradox, is listed as convergent). These methods allow the construction of solutions based on the conditions stipulated by Zeno, i.e. the amount of time taken at each step is geometrically decreasing.

Bertrand Russell

Bertrand Russell offered what is known as the "at-at theory of motion". It agrees that there can be no motion "during" a durationless instant, and contends that all that is required for motion is that the arrow be at one point at one time, at another point another time, and at appropriate points between those two points for intervening times. In this view motion is a function of position with respect to time.

Nick Huggett

Nick Huggett argues that Zeno is assuming the conclusion when he says that objects that occupy the same space as they do at rest must be at rest.

Peter Lynds

Peter Lynds has argued that all of Zeno's motion paradoxes are resolved by the conclusion that instants in time and instantaneous magnitudes do not physically exist. Lynds argues that an object in relative motion cannot have an instantaneous or determined relative position (for if it did, it could not be in motion), and so cannot have its motion fractionally dissected as if it does, as is assumed by the paradoxes. For more about the inability to know both speed and location, see Heisenberg uncertainty principle.

Hermann Weyl

Another proposed solution is to question one of the assumptions Zeno used in his paradoxes (particularly the Dichotomy), which is that between any two different points in space (or time), there is always another point. Without this assumption there are only a finite number of distances between two points, hence there is no infinite sequence of movements, and the paradox is resolved. The ideas of Planck length and Planck time in modern physics place a limit on the measurement of time and space, if not on time and space themselves. According to Hermann Weyl, the assumption that space is made of finite and discrete units is subject to a further problem, given by the "tile argument" or "distance function problem". According to this, the length of the hypotenuse of a right angled triangle in discretized space is always equal to the length of one of the two sides, in contradiction to geometry. Jean Paul Van Bendegem has argued that the Tile Argument can be resolved, and that discretization can therefore remove the paradox.

Hans Reichenbach

Hans Reichenbach has proposed that the paradox may arise from considering space and time as separate entities. In a theory like general relativity, which presumes a single space-time continuum, the paradox may be blocked.

The paradoxes in modern times

Infinite processes remained theoretically troublesome in mathematics until the late 19th century. The epsilon-delta version of Weierstrass and Cauchy developed a rigorous formulation of the logic and calculus involved. These works resolved the mathematics involving infinite processes.

While mathematics can calculate where and when the moving Achilles will overtake the Tortoise of Zeno's paradox, philosophers such as Brown and Moorcroft claim that mathematics does not address the central point in Zeno's argument, and that solving the mathematical issues does not solve every issue the paradoxes raise.

Popular literature often misrepresents Zeno's arguments. For example, Zeno is often said to have argued that the sum of an infinite number of terms must itself be infinite–with the result that not only the time, but also the distance to be travelled, become infinite. However, none of the original ancient sources has Zeno discussing the sum of any infinite series. Simplicius has Zeno saying "it is impossible to traverse an infinite number of things in a finite time". This presents Zeno's problem not with finding the sum, but rather with finishing a task with an infinite number of steps: how can one ever get from A to B, if an infinite number of (non-instantaneous) events can be identified that need to precede the arrival at B, and one cannot reach even the beginning of a "last event"?

Debate continues on the question of whether or not Zeno's paradoxes have been resolved. In The History of Mathematics: An Introduction (2010) Burton writes, "Although Zeno's argument confounded his contemporaries, a satisfactory explanation incorporates a now-familiar idea, the notion of a 'convergent infinite series.'".

Bertrand Russell offered a "solution" to the paradoxes based on the work of Georg Cantor, but Brown concludes "Given the history of 'final resolutions', from Aristotle onwards, it's probably foolhardy to think we've reached the end. It may be that Zeno's arguments on motion, because of their simplicity and universality, will always serve as a kind of 'Rorschach image' onto which people can project their most fundamental phenomenological concerns (if they have any)."

Pat Corvini offers a solution to the paradox of Achilles and the tortoise by first distinguishing the physical world from the abstract mathematics used to describe it. She claims the paradox arises from a subtle but fatal switch between the physical and abstract. Zeno's syllogism is as follows:

• P1: Achilles must first traverse an infinite number of divisions in order to reach the tortoise
• P2: it is impossible for Achilles to traverse an infinite number of divisions
• C: therefore, Achilles can never surpass the tortoise

Corvini shows that P1 is a mathematical abstraction which cannot be applied directly to P2 which is a statement regarding the physical world. The physical world requires a resolution amount used to distinguish distance while mathematics can use any resolution.

An ancient Chinese philosophic equivalent

Ancient Han Chinese philosophers from the Mohist School of Names during the Warring States period of China (479-221 BCE) independently developed equivalents to some of Zeno's paradoxes. The scientist and historian Sir Joseph Needham, in his well regarded academic work Science and Civilisation in China, describes an ancient Chinese paradox from the surviving Mohist School of Names book of logic which states, in the archaic ancient Chinese script, "a one-foot stick, every day take away half of it, in a myriad ages it will not be exhausted." Several other paradoxes from this philosophical school (more precisely, movement) are known, but their modern interpretation is more speculative.

Quantum Zeno effect

In 1977, physicists E. C. G. Sudarshan and B. Misra studying quantum mechanics discovered that the dynamical evolution (motion) of a quantum system can be hindered (or even inhibited) through observation of the system. This effect is usually called the "quantum Zeno effect" as it is strongly reminiscent of Zeno's arrow paradox. This effect was first theorized in 1958.

Zeno behaviour

In the field of verification and design of timed and hybrid systems, the system behaviour is called Zeno if it includes an infinite number of discrete steps in a finite amount of time. Some formal verification techniques exclude these behaviours from analysis, if they are not equivalent to non-Zeno behaviour.

In systems design these behaviours will also often be excluded from system models, since they cannot be implemented with a digital controller.